Statistical Inference

Group Model Inference

Table of contents

• Motivating Example
  • Species and Body Mass
  • Chest Pain and Heart Disease
• Model Inference
  • Model Inference
  • Model inference
  • Full and Reduced Model
  • Null and Alt Hypothesis
  • Group Model Inference
  • Group Full and Reduced Model
  • Group Null and Alt Hypothesis
• Family-wise Error Rate
  • Motivation
  • Type I Error and Its Rate
  • Definition of FWER
  • Why Control FWER?
  • Methods to Control FWER
• Linear Model Inference
  • Linear Model Inference
  • Linear Models: Difference Groups
  • ANOVA Table
  • Conducting an ANOVA in R
  • Species and Body Mass
  • Example: Hypothesis
  • Example: ANOVA
• Logistic Model Inference
  • Logistic Model Inference
  • Logistic Model Inference
  • Likelihood Ratio Test (Logistic)
  • Conducting an LRT in R
  • Chest Pain and Heart Disease
  • Example: Hypothesis
  • Example: LRT
• Post-Hoc Analysis
  • Post-Hoc Analysis
  • Group Proportions Or Means
  • Group Means
  • Group Proportions
  • Body Mass by Species
  • Heart Disease by Chest Pain
  • Multiple Comparisons Test
  • Multi-Comparison Test: Means
  • Multi-Comparison Test: Proportions
  • Body Mass by Species
  • Heart Disease by Chest Pain

Motivating Example

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Species and Body Mass

• Is there a difference in body mass between the penguins species?
• Is the difference due to a natural phenomenon or randomness?

penguins |> ggplot(aes(x=species, y = body_mass)) +
  geom_jitter() + 
  geom_boxplot() + 
  labs(x = "Species", y = "Body Mass")

Chest Pain and Heart Disease

• Is there a difference in proportions between the different chest pains?

• Is the difference due to a natural phenomenon or randomness?

heart_disease |> ggplot(aes(x=cp, fill = disease)) +
  geom_bar(position = "fill") +
  labs(x = "Chest Pain") + 
  theme(axis.text.x = element_text(size = 14)) 

Model Inference

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Model Inference

Model Inference is the act of conducting a hypothesis test on the entire model (line). We do this to determine if the fully explained model is significantly different from the smaller models or average.

Model inference determines if more variation is explained by including more predictors.

Model inference

• We will conduct model inference to determine if different models are better at explaining variation. Both Linear and Logistic Regression have techniques to test different models.

• For Linear Regression, we determine the significance of the variation explained using an Analysis of Variance (ANOVA) table and F test.

• For Logistic Regression, we determine the significance of the variation explained using a Likelihood Ratio test.

• Conducting Model Inference first ensures that the Family-wise Error Rate is controlled.

Full and Reduced Model

Full Model

\[ Y = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p \]

Reduced Model

\[ Y = \beta_0 + \beta_1 X_1 \]

Null and Alt Hypothesis

\(H_0\): The fully-parameterized model does not explain more variation than the reduced model.

\(H_a\): The fully-parameterized model does explain more variation than the reduced model.

Group Model Inference

• Group Model Inference tests whether a categorical variable significantly reduces the variation of the outcome of interest.

• This tells us if the group means are different from each other.

Group Full and Reduced Model

Full Model

\[ Y = \beta_0 + \beta_1 C_1 + \cdots + \beta_p C_p \]

Reduced Model

\[ Y = \bar Y \]

Group Null and Alt Hypothesis

\(H_0\): The different categories do not have significantly different means/proportions from each other.

\(H_a\): At least two categories have significantly different means/proportions from each other.

Family-wise Error Rate

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Motivation

• In multiple hypothesis testing, we test several hypotheses simultaneously.
• The probability of making at least one Type I error increases with the number of tests.
• Hence, we need error control methods.

Type I Error and Its Rate

Type I Error (False Positive): Rejecting a null hypothesis (\(H_0\)), when it is true.

Type I Error Rate (\(\alpha\)): The probability of making a Type I error in a single hypothesis test.

\[ \alpha = P(\text{Reject } H_0 \mid H_0 \text{ is true}) \]

Typically, \(\alpha = 0.05\), meaning a 5% chance of incorrectly rejecting a true null hypothesis.

Definition of FWER

Family-Wise Error Rate (FWER): The probability of making one or more Type I errors among all hypotheses tested.

\[ \text{FWER} = P(\text{At least one false rejection}) = P(V \ge 1) \]

where:

• \(V\) = number of false positives (incorrect rejections)

Why Control FWER?

• Maintains overall confidence in conclusions.
• Avoids claiming false discoveries when many tests are run.
• Trade-off: Strong control of FWER reduces power (increases Type II error).

Methods to Control FWER

1. Bonferroni Correction

2. Holm-Bonferroni Procedure (Step-down)

3. Tukey’s Honest Significant Difference (HSD)

Linear Model Inference

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Linear Model Inference

Given 2 models:

\[ \hat Y = \hat\beta_0 + \hat\beta_1 X_1 + \hat\beta_2 X_2 + \cdots + \hat\beta_p X_p \]

or

\[ \hat Y = \bar y \]

Is the model with predictors do a better job than using the average?

Linear Models: Difference Groups

Given a categorical variable with 4 categories, which model is better:

\[ \hat Y = \hat\beta_0 + \hat\beta_1 C_1 + \hat\beta_2 C_2 + \hat\beta_3 C_3 \]

or

\[ \hat Y = \bar y \]

Are the 2 models different from each other?

ANOVA Table

Source	DF	SS	MS	F
Model	\(DFR=k-1\)	\(SSR\)	\(MSR=\frac{SSM}{DFR}\)	\(\hat F=\frac{MSR}{MSE}\)
Error	\(DFE=n-k\)	\(SSE\)	\(MSE=\frac{SSE}{DFE}\)
Total	\(TDF=n-1\)	\(TSS=SSR+SSE\)

\[ \hat F \sim F(DFR, DFE) \]

Conducting an ANOVA in R

xlm <- lm(Y ~ X, data = DATA)
anova(xlm)

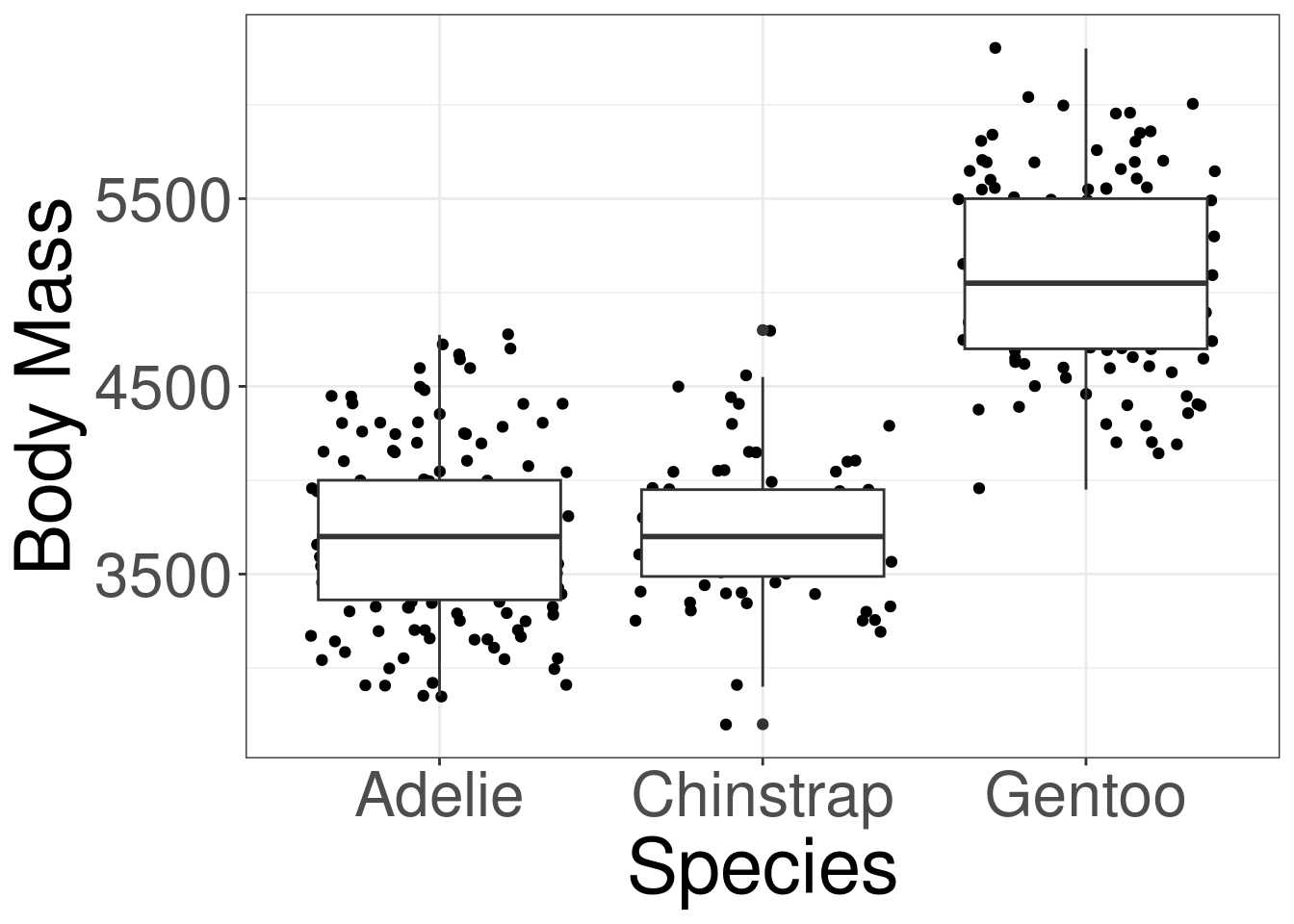
• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Species and Body Mass

• Is there a difference in body mass between the penguins species?
• Is the difference due to a natural phenomenon or randomness?

penguins |> ggplot(aes(x=species, y = body_mass)) +
  geom_jitter() + 
  geom_boxplot() + 
  labs(x = "Species", y = "Body Mass")

Example: Hypothesis

• \(H_0\): The mean body mass are the same between the 3 penguin species.

• \(H_1\): At least one species pairing have different mean body mass.

Example: ANOVA

xlm <- lm(body_mass ~ species, data = penguins)
anova(xlm)

#> Analysis of Variance Table
#> 
#> Response: body_mass
#>            Df    Sum Sq  Mean Sq F value    Pr(>F)    
#> species     2 145190219 72595110  341.89 < 2.2e-16 ***
#> Residuals 330  70069447   212332                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Logistic Model Inference

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Logistic Model Inference

Given 2 models:

\[ g(\hat Y) = \hat\beta_0 + \hat\beta_1 X_1 + \hat\beta_2 X_2 + \cdots + \hat\beta_p X_p \]

or

\[ g(\hat Y) = \bar y \]

Is the model with predictors do a better job than using the average?

Logistic Model Inference

Given a categorical variable with 4 categories, which model is better:

\[ g(\hat Y) = \hat\beta_0 + \hat\beta_1 C_1 + \hat\beta_2 C_2 + \hat\beta_3 C_3 \]

or

\[ g(\hat Y) = \bar y \]

Are the 2 models different from each other?

Likelihood Ratio Test (Logistic)

The Likelihood Ratio Test is a test to determine whether the likelihood of observing the outcome is significantly bigger in a larger, more complicated model, than a simpler model.

It conducts a hypothesis tests to see if models are significantly different from each other.

Conducting an LRT in R

xlm <- glm(Y ~ X, data = DATA, family = binomial)
anova(xlm)

• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Chest Pain and Heart Disease

• Is there a difference in proportions between the different chest pains?

• Is the difference due to a natural phenomenon or randomness?

heart_disease |> ggplot(aes(x=cp, fill = disease)) +
  geom_bar(position = "fill") +
  labs(x = "Chest Pain") + 
  theme(axis.text.x = element_text(size = 14)) 

Example: Hypothesis

• \(H_0\): The proportion of having heart disease are the same between the 4 chest pain types.

• \(H_1\): At least one chest pain pairing have different proportions of having heart disease.

Example: LRT

xglm <- glm(disease ~ cp, data = heart_disease,
            family = binomial)
anova(xglm)

#> Analysis of Deviance Table
#> 
#> Model: binomial, link: logit
#> 
#> Response: disease
#> 
#> Terms added sequentially (first to last)
#> 
#> 
#>      Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
#> NULL                   296     409.95              
#> cp    3   81.195       293     328.75 < 2.2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Post-Hoc Analysis

• Motivating Example

• Model Inference

• Family-wise Error Rate

• Linear Model Inference

• Logistic Model Inference

• Post-Hoc Analysis

Post-Hoc Analysis

• If we found to reject the null hypothesis from our model inference, we conduct a post-hoc analysis to determine which groups are significantly different from each other.

• We will conduct multiple comparisons test, while maintaining the family-wise error rate, to determine which groups are different from each other.

Group Proportions Or Means

We will use the emmeans function from the emmeans R package to obtain the group proportions or means.

Group Means

m <- lm(Y ~ X, data = DATA)
emmeans(m, ~X)

• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Group Proportions

m <- glm(Y ~ X, data = DATA, family = binomial)
emmeans(m, ~X, type = "response")

• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Body Mass by Species

m1 <- lm(body_mass ~ species, data = penguins)
emmeans(m1, ~species)

#>  species   emmean   SE  df lower.CL upper.CL
#>  Adelie      3706 38.1 330     3631     3781
#>  Chinstrap   3733 55.9 330     3623     3843
#>  Gentoo      5092 42.2 330     5009     5176
#> 
#> Confidence level used: 0.95

Heart Disease by Chest Pain

m2 <- glm(disease ~ cp, data = heart_disease, family = binomial)
emmeans(m2, ~ cp, type = "response")

#>  cp                prob     SE  df asymp.LCL asymp.UCL
#>  Asymptomatic     0.725 0.0375 Inf    0.6463     0.792
#>  Atypical Angina  0.184 0.0553 Inf    0.0984     0.317
#>  Non-anginal Pain 0.217 0.0452 Inf    0.1411     0.318
#>  Typical Angina   0.304 0.0959 Inf    0.1525     0.515
#> 
#> Confidence level used: 0.95 
#> Intervals are back-transformed from the logit scale

Multiple Comparisons Test

• A multi-comparison test can be achieved by using the pairs function from the output of the emmeans function.

• This function will automatically adjust the p-values using Tukey’s method to fix the family-wise error rate.

Multi-Comparison Test: Means

m <- lm(Y ~ X, data = DATA)
e <- emmeans(m, ~X)
pairs(e)

• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Multi-Comparison Test: Proportions

m <- glm(Y ~ X, data = DATA, family = binomial)
e <- emmeans(m, ~X, type = "response")
pairs(e)

• Y: Outcome variable in DATA
• X: Categorical variable in DATA
• DATA: Name of the data (frame) set

Body Mass by Species

m1 <- lm(body_mass ~ species, data = penguins)
e1 <- emmeans(m1, ~species)
pairs(e1)

#>  contrast           estimate   SE  df t.ratio p.value
#>  Adelie - Chinstrap    -26.9 67.7 330  -0.398  0.9164
#>  Adelie - Gentoo     -1386.3 56.9 330 -24.359 <0.0001
#>  Chinstrap - Gentoo  -1359.3 70.0 330 -19.406 <0.0001
#> 
#> P value adjustment: tukey method for comparing a family of 3 estimates

Heart Disease by Chest Pain

m2 <- glm(disease ~ cp, data = heart_disease, family = binomial)
e2 <- emmeans(m2, ~ cp, type = "response")
pairs(e2)

#>  contrast                             odds.ratio    SE  df null z.ratio p.value
#>  Asymptomatic / Atypical Angina           11.738 4.860 Inf    1   5.948 <0.0001
#>  Asymptomatic / (Non-anginal Pain)         9.537 3.110 Inf    1   6.917 <0.0001
#>  Asymptomatic / Typical Angina             6.037 2.960 Inf    1   3.664  0.0014
#>  Atypical Angina / (Non-anginal Pain)      0.812 0.370 Inf    1  -0.456  0.9684
#>  Atypical Angina / Typical Angina          0.514 0.301 Inf    1  -1.138  0.6660
#>  (Non-anginal Pain) / Typical Angina       0.633 0.333 Inf    1  -0.870  0.8204
#> 
#> P value adjustment: tukey method for comparing a family of 4 estimates 
#> Tests are performed on the log odds ratio scale