Statistical Inference

Model Inference

Table of contents

• Hypothesis Tests: Multi Regression
  • Hypothesis Tests
  • Hypothesis Testing Steps
  • Null Hypothesis \(H_0\)
  • Alternative Hypothesis \(H_1\)
  • Significance Level
  • Conducting HT of \(\beta_j\) Linear R
  • Conducting HT of \(\beta_j\)
• Examples
  • Penguins Example
  • Penguins: Hypothesis
  • Penguins: \(\alpha\)-level
  • Penguins: Code
  • Penguins: Decision Making
  • Penguins: Interpretation
  • Heart Disease Example
  • Heart: Hypothesis
  • Heart: \(\alpha\)-level
  • Heart: Code
  • Heart: Decision Making
  • Heart: Interpretation
• Power Analysis
  • What is Statistical Power
  • Why Power Matters
  • Errors in Inference
  • Type I Error (False Positive)
  • Type II Error (False Negative)
  • Balancing Errors
  • What Affects Power?
  • Boosting Power
• Model Conditions
  • Model Conditions
  • Linearity
  • Independence
  • Probability Assumption
  • Equal Variances
  • Residuals
  • Influential Measurements
  • Raw Residuals
  • Residual Analysis
  • QQ Plot
  • Residual vs Fitted Plot
  • Residual Analysis in R
  • Residual vs Fitted Plot
  • QQ Plot
  • Penguins: Example
  • Heart: Example

Hypothesis Tests: Multi Regression

• Hypothesis Tests: Multi Regression

• Examples

• Power Analysis

• Model Conditions

Hypothesis Tests

Conducting a hypothesis test for coefficients in regression models with more than one predictor is the same as the standard simple approaches.

You will just need to specify the hypothesis tests are adjusted for the other covariates.

Hypothesis Testing Steps

1. State \(H_0\) and \(H_1\)
2. Choose \(\alpha\)
3. Compute confidence interval/p-value
4. Make a decision

Null Hypothesis \(H_0\)

The null hypothesis is the claim that is initially believed to be true. For the most part, it is always equal to the hypothesized value.

Alternative Hypothesis \(H_1\)

The alternative hypothesis contradicts the null hypothesis.

Significance Level

Choose a value that represents the probability of being wrong if you decide to reject the \(H_0\).

\[ \alpha = 0.05 \]

Walk through the steps slowly with an example in mind. Emphasize that \(\alpha\) is a threshold, not the actual probability of error.

Conducting HT of \(\beta_j\) Linear R

XLM <- lm(Y ~ X1 + X2 + ... + Xp, data = DATA)
tidy(XLM)

• XLM: Object where the model is stored
• Y: Name of the outcome variable in DATA
• X1, X2, …, Xp: predictor variables in DATA
• DATA: Name of the data set

Conducting HT of \(\beta_j\)

XLM <- glm(Y ~ X1 + X2 + ... + Xp, data = DATA, family = binomial())
tidy(XLM)

• XLM: Object where the model is stored
• Y: Name of the outcome variable in DATA
• X1, X2, …, Xp: predictor variables in DATA
• DATA: Name of the data set

Examples

• Hypothesis Tests: Multi Regression

• Examples

• Power Analysis

• Model Conditions

Penguins Example

Is there a significant relationship between penguin body mass (outcome; body_mass) and flipper length (predictor; flipper_len), adjusting for species? Use the penguins data set to determine a significant association.

Penguins: Hypothesis

\(H_0\): There is no relationship between penguin body mass and flipper length, adjusting for penguin species (\(\beta_{flipper\_len} = 0\))

\(H_1\): There is a relationship between penguin body mass and flipper length, adjusting for penguin species (\(\beta_{flipper\_len} \ne 0\))

Penguins: \(\alpha\)-level

\[ \alpha = 0.05 = 5.0*10^{-2} = 5.0e-2 \]

Penguins: Code

m1 <- lm(body_mass ~ flipper_len + species, penguins)
tidy(m1)

#> # A tibble: 4 × 5
#>   term             estimate std.error statistic  p.value
#>   <chr>               <dbl>     <dbl>     <dbl>    <dbl>
#> 1 (Intercept)       -4031.     584.       -6.90 2.55e-11
#> 2 flipper_len          40.7      3.07     13.3  1.40e-32
#> 3 speciesChinstrap   -207.      57.7      -3.58 3.98e- 4
#> 4 speciesGentoo       267.      95.3       2.80 5.39e- 3

Penguins: Decision Making

\[ p = 1.4e-32 < 5e-2 = 0.05 = \alpha \]

Reject \(H_0\)

Penguins: Interpretation

There is a significant association between penguins flipper length and body mass, after adjusting for species (p < 0.0001; \(\beta = 40.7\)). As flipper length increases by 1 unit, body mass increases by 40.7 units, adjusting for penguin species.

Heart Disease Example

Is there a significant association between heart disease (outcome; disease) and resting blood pressure (predictor; trestbps), adjusting for chest pain (cp). Use the heart_disease data set to determine a significant association.

Heart: Hypothesis

\(H_0\): There is no relationship between heart disease probability and resting blood pressure, adjusting for chest pain (\(\beta_{bp} = 0\))

\(H_1\): There is no relationship between heart disease probability and resting blood pressure, adjusting for chest pain (\(\beta_{bp} \ne 0\))

Heart: \(\alpha\)-level

\[ \alpha = 0.05 = 5.0*10^{-2} = 5.0e-2 \]

Heart: Code

m2 <- glm(disease ~ trestbps + cp, heart_disease, family = binomial())
tidy(m2)

#> # A tibble: 5 × 5
#>   term        estimate std.error statistic   p.value
#>   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
#> 1 (Intercept)  -3.80     1.25       -3.04  0.00234  
#> 2 trestbps      0.0209   0.00807     2.59  0.00967  
#> 3 cp2          -0.409    0.601      -0.681 0.496    
#> 4 cp3          -0.236    0.540      -0.437 0.662    
#> 5 cp4           2.04     0.512       3.99  0.0000674

Heart: Decision Making

\[ p = 0.00967 < 0.05 = \alpha \]

Reject \(H_0\)

Heart: Interpretation

There is a significant association between heart disease and resting blood pressure, after adjusting for chest pain (p < 0.00967; \(\beta = 0.0209\)). As resting blood pressure increases by 1 unit, the odds of having heart disease increases by a factor of 1.02, adjusting for chest pain.

Power Analysis

• Hypothesis Tests: Multi Regression

• Examples

• Power Analysis

• Model Conditions

What is Statistical Power

• Statistical Power is the probability of correctly rejecting a false null hypothesis.
• In other words, it’s the chance of detecting a real effect when it exists.

Why Power Matters

• Low power → high risk of Type II Error (false negatives)
• High power → better chance of finding true effects
• Common threshold: 80% power

Errors in Inference

Type I	Reject \(H_0\) when true	False positive
Type II	Don’t reject \(H_0\) when false	False negative
Power	\(1 - P(\text{Type II})\)	Detecting a true effect

Power is often overlooked. It’s about how sensitive the test is to real effects. Larger samples increase power.

Type I Error (False Positive)

• Rejecting \(H_0\) when it is actually true
• Probability = \(\alpha\) (significance level)

Type I errors happen when we detect an effect that doesn’t really exist. This is controlled by our chosen alpha level.

Type II Error (False Negative)

• Failing to reject \(H_0\) when it is actually false
• Probability = \(\beta\)
• Power = \(1 - \beta\)

Type II errors are often due to small sample sizes or high variability. Power analysis helps us plan to avoid these.

Balancing Errors

• Lowering \(\alpha\) reduces Type I errors, but increases risk of Type II errors.
• To reduce both:
  • Increase sample size
  • Use more appropriate statistical tests

There’s a trade-off between these errors. We can’t eliminate both, but we can manage the risk based on the consequences of each type.

What Affects Power?

1. Effect Size
   • Bigger effects are easier to detect
2. Sample Size (\(n\))
   • Larger samples reduce standard error
3. Significance Level (\(\alpha\))
   • Higher \(\alpha\) increases power (but riskier!)
4. Variability
   • Less noise in data = better power

Boosting Power

• Power = Probability of rejecting \(H_0\) when it’s false
• Helps avoid Type II Errors
• Driven by:
  • Sample size
  • Effect size
  • \(\alpha\)
  • Variability
• Aim for 80% or higher

Model Conditions

• Hypothesis Tests: Multi Regression

• Examples

• Power Analysis

• Model Conditions

Model Conditions

When we are conducting inference with regression models, we will have to check the following conditions:

• Linearity
• Independence
• Probability Assumption
• Equal Variances
• Multicollinearity (for Multi-Regression)

Linearity

There must be a linear relationship between both the outcome variable (y) and a set of predictors (\(x_1\), \(x_2\), …).

Independence

The data points must not influence each other.

Probability Assumption

The model errors (also known as residuals) must follow a specified distribution.

• Linear Regression: Normal Distribution

• Logistic Regression: Binomial Distribution

Equal Variances

The variability of the data points must be the same for all predictor values.

Residuals

Residuals are the errors between the observed value and the estimated model. Common residuals include

• Raw Residual

• Standardized Residuals

• Jackknife (studentized) Residuals

• Deviance Residuals

• Quantized Residuals

Influential Measurements

Influential measures are statistics that determine how much a data point affects the model. Common influential measures are

• Leverages

• Cook’s Distance

Raw Residuals

\[ \hat r_i = y_i - \hat y_i \]

Residual Analysis

A residual analysis is used to test the assumptions of linear regression.

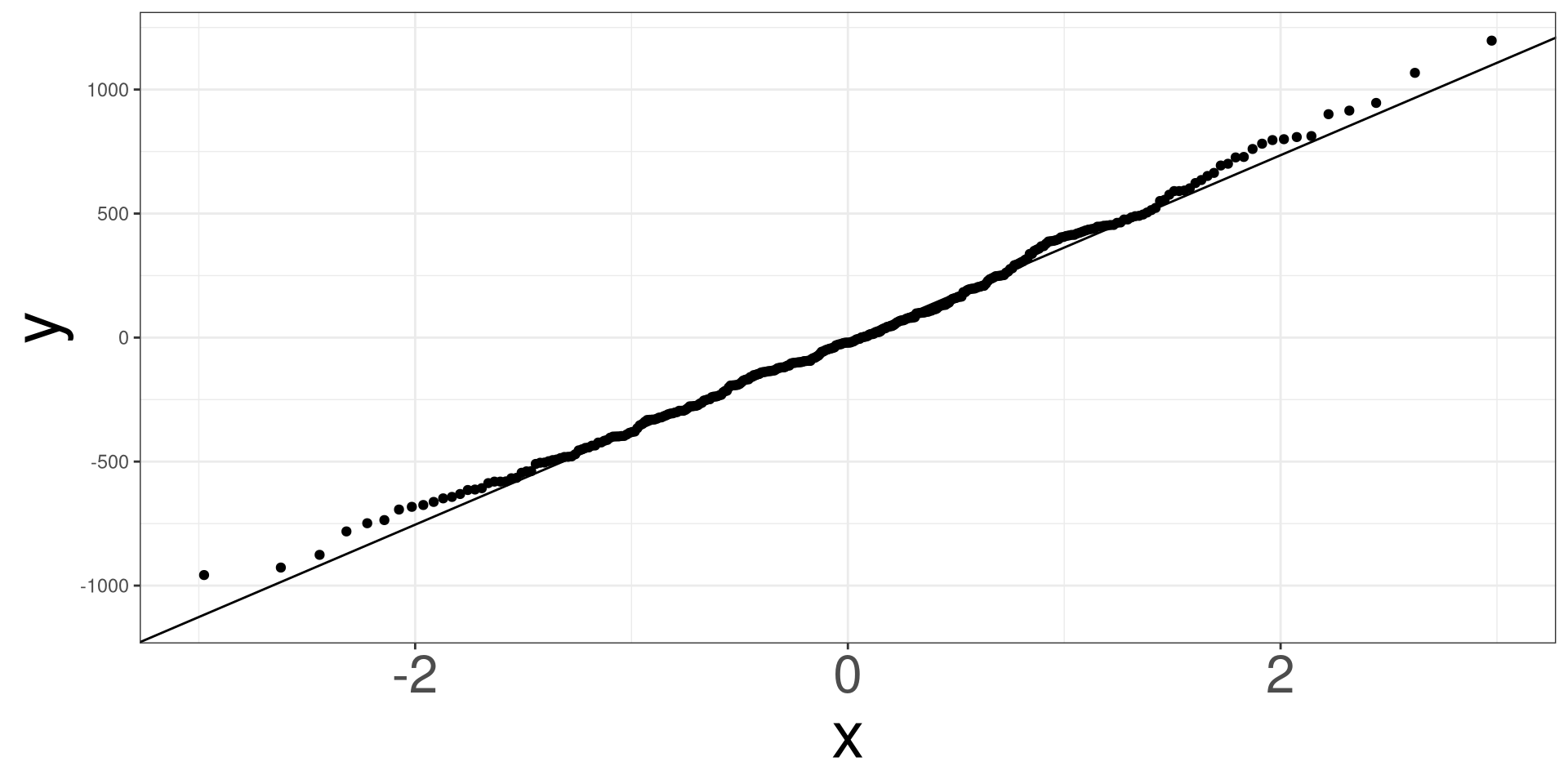
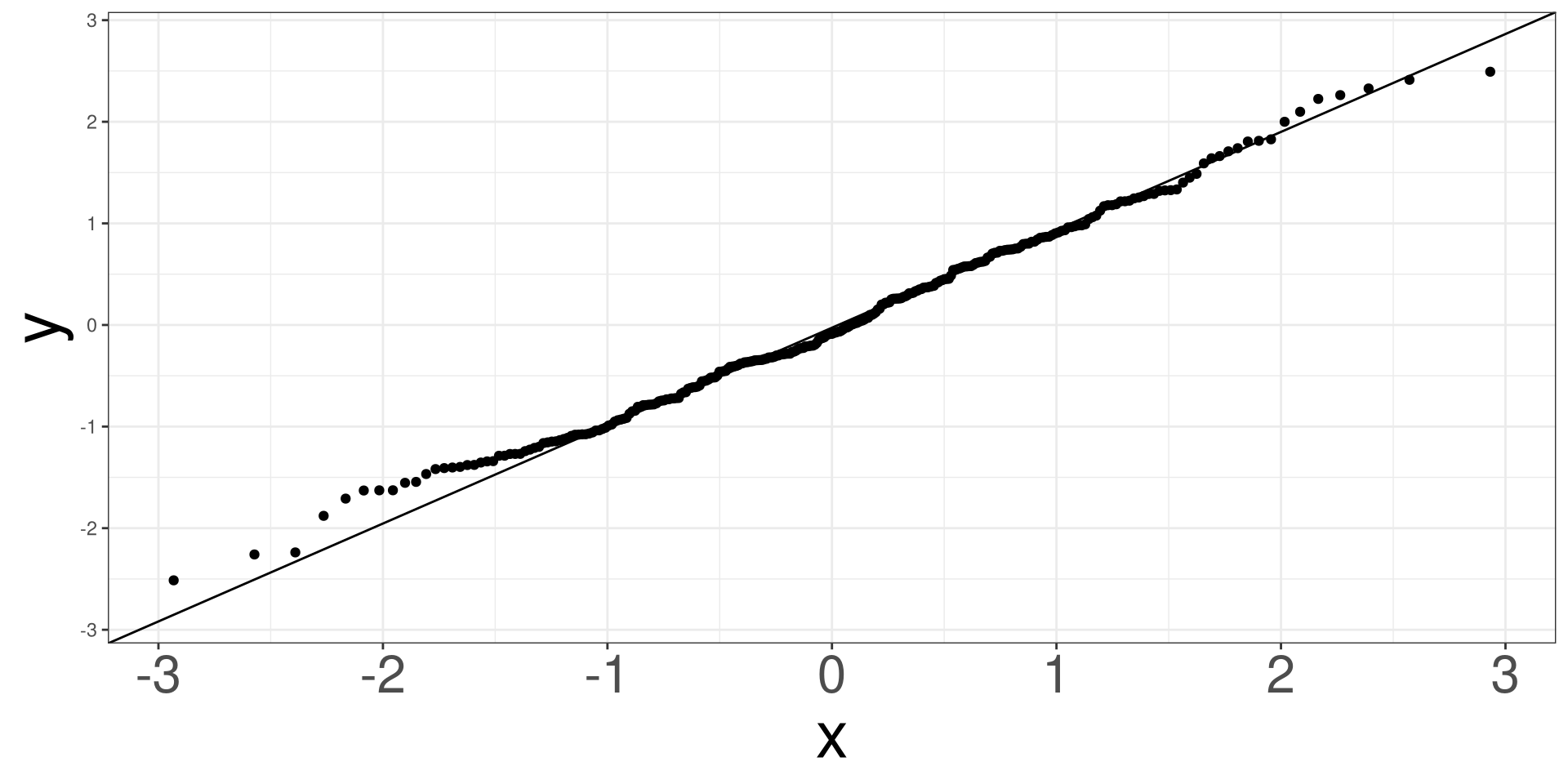
QQ Plot

A qq (quantile-quantile) plot will plot the estimated quantiles of the residuals against the theoretical quantiles from a normal distribution function. If the points from the qq-plot lie on the \(y=x\) line, it is said that the residuals follow a normal distribution.

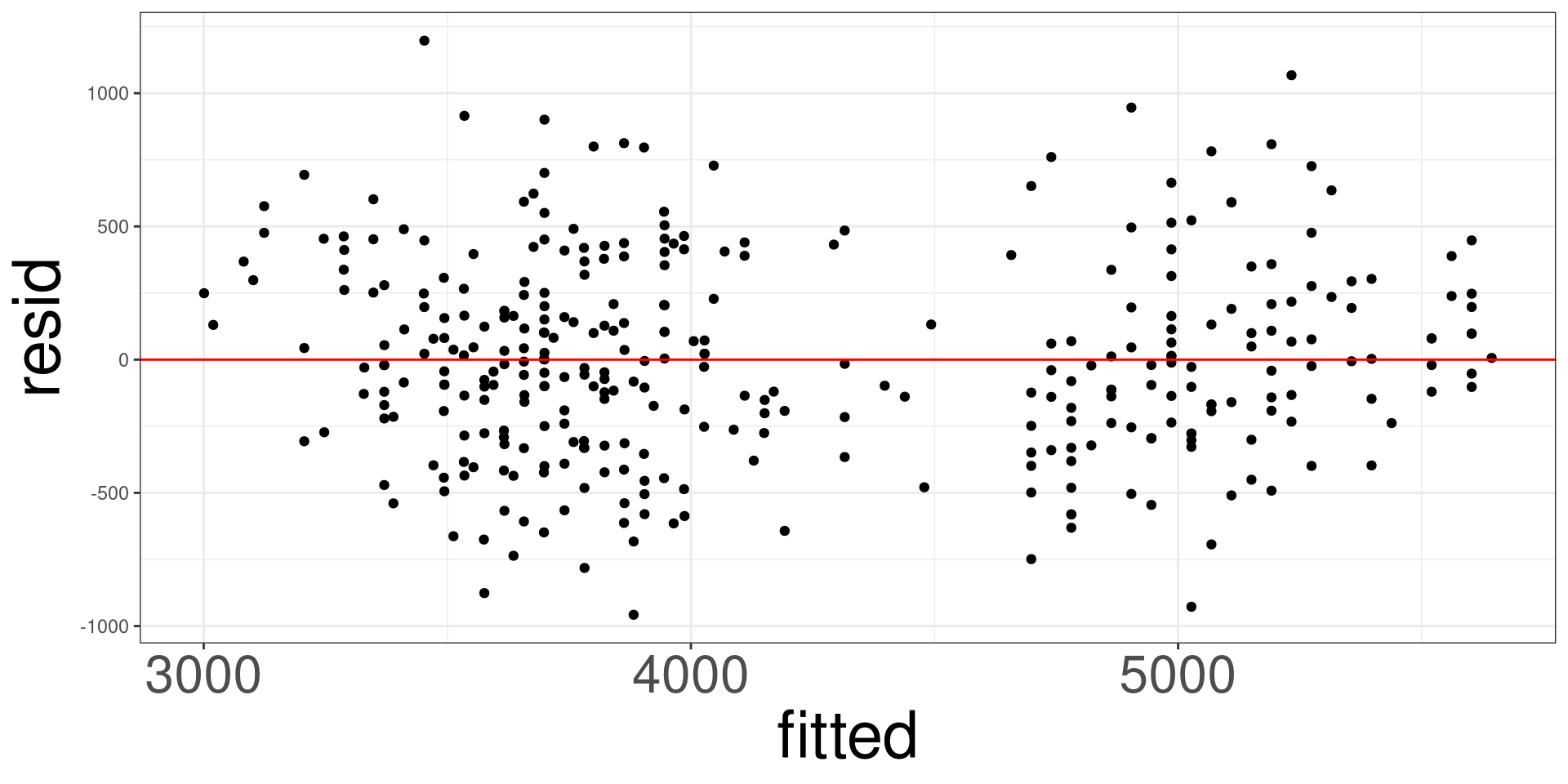
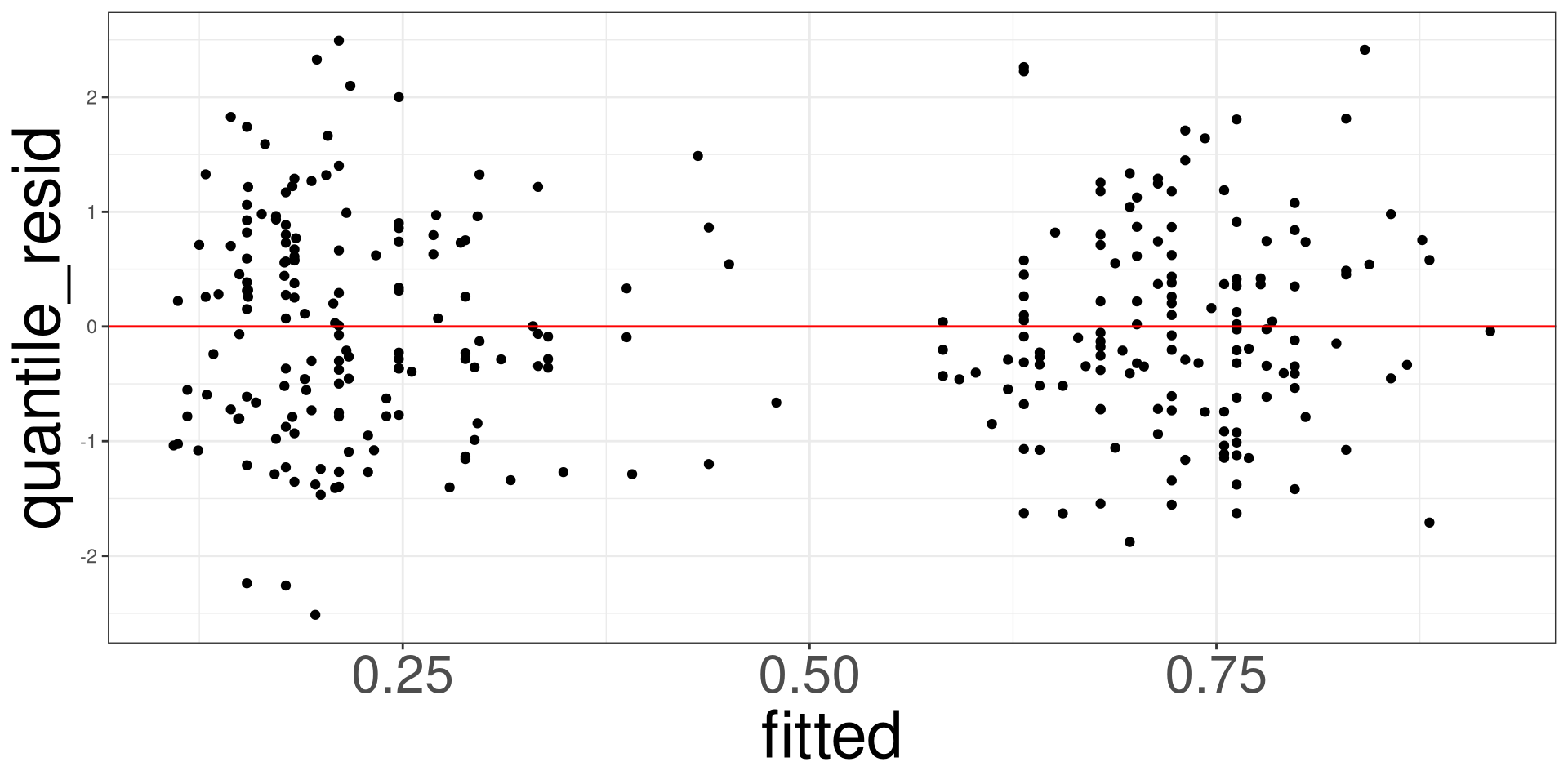
Residual vs Fitted Plot

This plot allows you to assess the linearity, constant variance, and identify potential outliers. Create a scatter plot between the fitted values (x-axis) and the raw/standardized residuals (y-axis).

Residual Analysis in R

Use the resid_df function to obtain the residuals of a model.

rdf <- resid_df(OBJECT)

Residual vs Fitted Plot

Linear

ggplot(RDF, aes(fitted, resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

Logistic

ggplot(RDF, aes(fitted, quantile_resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

• RDF: Name of object from resid_df()

QQ Plot

Linear

ggplot(RDF, aes(sample = resid)) + 
  stat_qq() +
  stat_qq_line() 

Logistic

ggplot(RDF, aes(sample = quantile_resid)) + 
  stat_qq() +
  stat_qq_line() 

• RDF: Name of object from resid_df()

Penguins: Example

m3 <- lm(body_mass ~   island + species + flipper_len,
          penguins)
tidy(m3)

#> # A tibble: 6 × 5
#>   term             estimate std.error statistic  p.value
#>   <chr>               <dbl>     <dbl>     <dbl>    <dbl>
#> 1 (Intercept)       -4048.     586.      -6.91  2.40e-11
#> 2 islandDream         -59.8     75.7     -0.789 4.31e- 1
#> 3 islandTorgersen    -102.      77.7     -1.31  1.90e- 1
#> 4 speciesChinstrap   -206.      70.4     -2.92  3.71e- 3
#> 5 speciesGentoo       200.     110.       1.82  6.94e- 2
#> 6 flipper_len          41.1      3.09    13.3   9.26e-33

dfm3 <- resid_df(m3)
head(dfm3)

#>   obs body_mass    island species flipper_len     resid   fitted      sresid
#> 1   1      3750 Torgersen  Adelie         181  462.5612 3287.439  1.24797225
#> 2   2      3800 Torgersen  Adelie         186  307.1225 3492.877  0.82640213
#> 3   3      3250 Torgersen  Adelie         195 -612.6671 3862.667 -1.64784619
#> 5   4      3450 Torgersen  Adelie         193 -330.4916 3780.492 -0.88855590
#> 6   5      3650 Torgersen  Adelie         190   -7.2284 3657.228 -0.01943297
#> 7   6      3625 Torgersen  Adelie         181  337.5612 3287.439  0.91072706
#>      hatvals   jackknife        cooks
#> 1 0.02662612  1.24901185 7.100464e-03
#> 2 0.02143054  0.82601134 2.492718e-03
#> 3 0.02058469 -1.65208143 9.511731e-03
#> 5 0.01982753 -0.88827691 2.661855e-03
#> 6 0.01970442 -0.01940404 1.265126e-06
#> 7 0.02662612  0.91049529 3.781407e-03

ggplot(dfm3, aes(fitted, resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

ggplot(dfm3, aes(sample = resid)) + 
  stat_qq() +
  stat_qq_line() 

Heart: Example

m4 <- glm(disease ~ trestbps + cp, heart_disease, family = binomial())
tidy(m4)

#> # A tibble: 5 × 5
#>   term        estimate std.error statistic   p.value
#>   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
#> 1 (Intercept)  -3.80     1.25       -3.04  0.00234  
#> 2 trestbps      0.0209   0.00807     2.59  0.00967  
#> 3 cp2          -0.409    0.601      -0.681 0.496    
#> 4 cp3          -0.236    0.540      -0.437 0.662    
#> 5 cp4           2.04     0.512       3.99  0.0000674

dfm4 <- resid_df(m4)
head(dfm4)

#>   obs disease trestbps cp    fitted        eta  raw_resid pearson_resid
#> 1   1      no      145  1 0.3162617 -0.7710053 -0.3162617    -0.6801087
#> 2   2     yes      160  4 0.8296967  1.5834796  0.1703033     0.4530559
#> 3   3     yes      120  4 0.6787886  0.7482102  0.3212114     0.6879046
#> 4   4      no      130  3 0.2107532 -1.3203915 -0.2107532    -0.5167502
#> 5   5      no      130  2 0.1834250 -1.4933128 -0.1834250    -0.4739486
#> 6   6      no      120  2 0.1541873 -1.7021301 -0.1541873    -0.4269600
#>   deviance_resid working_resid partial_resid.trestbps partial_resid.cp
#> 1     -0.8719863     -2.233553              -1.184687        -2.305014
#> 2      0.6110565      2.788739               1.796346         2.404052
#> 3      0.8802790      2.221423               1.229030         2.672005
#> 4     -0.6880061     -2.587422              -1.302396        -2.345657
#> 5     -0.6366106     -2.717940              -1.259993        -2.476175
#> 6     -0.5787181     -2.884425              -1.426478        -2.433842
#>   std_pear_resid std_dev_resid stud_dev_resid quantile_resid   leverages
#> 1     -0.6962858    -0.8927274     -0.8846616     -1.3402462 0.045927133
#> 2      0.4562301     0.6153377      0.6134136      0.4534013 0.013866647
#> 3      0.6910541     0.8843093      0.8827424      0.2192157 0.009094376
#> 4     -0.5199246    -0.6922325     -0.6903935     -0.3003890 0.012173676
#> 5     -0.4789686    -0.6433536     -0.6403567      0.3764186 0.020852010
#> 6     -0.4311339    -0.5843756     -0.5818043      0.1518214 0.019268922
#>          cooks
#> 1 0.0046675922
#> 2 0.0005853744
#> 3 0.0008765864
#> 4 0.0006662724
#> 5 0.0009771107
#> 6 0.0007304018

ggplot(dfm4, aes(fitted, quantile_resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

ggplot(dfm4, aes(sample = quantile_resid)) + 
  stat_qq() +
  stat_qq_line()