Inference with Linear Regression

2025-04-21

Motivating Example

• Motivating Example

• Mathematical Models

• \(\beta\) Hypothesis Testing

• Model Hypothesis Testing

• Model Assumptions

Motivating Example

p1 <- penguins |> ggplot(aes(x=species, y = body_mass_g)) +
  geom_jitter() + 
  geom_boxplot() + 
  labs(x = "Species", y = "Body Mass")
  
p2 <- penguins |> ggplot(aes(x=flipper_length_mm, y = body_mass_g)) +
  geom_point() + 
  labs(x = "Flipper Length", y = "Body Mass")  

p1 + p2

Mathematical Models

• Motivating Example

• Mathematical Models

• \(\beta\) Hypothesis Testing

• Model Hypothesis Testing

• Model Assumptions

Mathematical Models

Standard Normal Distribution

\[ {\frac{1}{\sqrt{2 \pi}}} e^{-\frac{1}{2}x^2} \]

data.frame(x = seq(-5,5, length.out = 100), 
           y1 = dt(seq(-5,5, length.out = 100), 1),
           y2 = dt(seq(-5,5, length.out = 100), 10),
           y3 = dt(seq(-5,5, length.out = 100), 30),
           y4 = dt(seq(-5,5, length.out = 100), 100),
           y5 = dnorm((seq(-5,5, length.out = 100)))) |> 
  ggplot() +
  # geom_line(aes(x, y1, color = "1")) +
  # geom_line(aes(x, y2, color = "10")) +
  # geom_line(aes(x, y3, color = "30")) +
  # geom_line(aes(x, y4, color = "100")) +
  geom_line(aes(x, y5)) +
  ylab("y")

t Distribution

\[ \frac{\Gamma \left(\frac{v+1}{2}\right)}{\sqrt{\pi v}\Gamma\left(\frac{v}{2}\right)} \left(1 + \frac{x^2}{v}\right)^{-\frac{v+1}{2}} \]

data.frame(x = seq(-5,5, length.out = 100), 
           y1 = dt(seq(-5,5, length.out = 100), 1),
           y2 = dt(seq(-5,5, length.out = 100), 10),
           y3 = dt(seq(-5,5, length.out = 100), 30),
           y4 = dt(seq(-5,5, length.out = 100), 100),
           y5 = dnorm((seq(-5,5, length.out = 100)))) |> 
  ggplot() +
  geom_line(aes(x, y1, color = "1")) +
  geom_line(aes(x, y2, color = "10")) +
  geom_line(aes(x, y3, color = "30")) +
  geom_line(aes(x, y4, color = "100")) +
  geom_line(aes(x, y5, color = "Normal")) +
  ylab("y")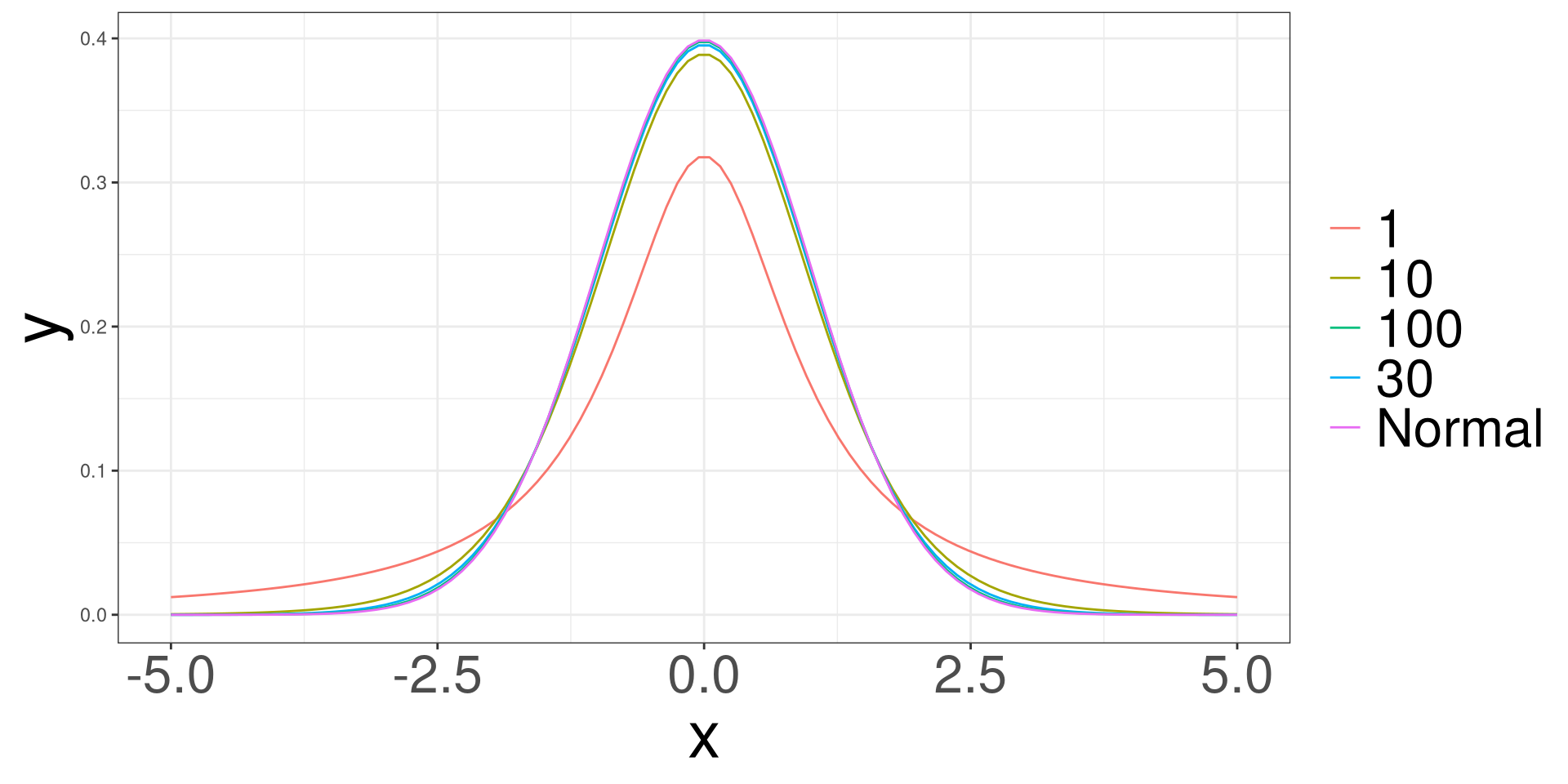

\(\beta\) Hypothesis Testing

• Motivating Example

• Mathematical Models

• \(\beta\) Hypothesis Testing

• Model Hypothesis Testing

• Model Assumptions

Hypothesis

\[H_0: \beta = \theta\]

\[H_0: \beta \ne \theta\]

Testing \(\beta_j\)

\[ T = \frac{\hat\beta_j-\theta}{\mathrm{se}(\hat\beta_j)} \sim t_{n-p^\prime} \]

• \(n\): sample size
• \(p^\prime\): number of \(\beta\)s

P-Value

Alternative Hypothesis	p-value
\(\beta>\theta\)	\(P(\hat\beta >T)=p\)
\(\beta<\theta\)	\(P(\hat\beta < T)=p\)
\(\beta\ne\theta\)	\(2\times P(\hat\beta >|T|)=p\)

Confidence Intervals

\[ \hat \beta_j \pm CV \times se(\hat\beta_j) \]

• \(CV\): Critical Value \(P(X<CV) = 1-\alpha/2\)

• \(\alpha\): significance level

• \(se\): Standard Error Function

Conducting HT of \(\beta_j\)

xlm <- lm(Y ~ X, data = DATA)
summary(xlm)

Example

m1 <- lm(body_mass_g ~ species + flipper_length_mm, penguins)
summary(m1)

#> 
#> Call:
#> lm(formula = body_mass_g ~ species + flipper_length_mm, data = penguins)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -898.8 -252.0  -24.8  229.8 1191.6 
#> 
#> Coefficients:
#>                   Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)       -4013.18     586.25  -6.846 3.74e-11 ***
#> speciesChinstrap   -205.38      57.57  -3.568 0.000414 ***
#> speciesGentoo       284.52      95.43   2.981 0.003083 ** 
#> flipper_length_mm    40.61       3.08  13.186  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 373.3 on 329 degrees of freedom
#> Multiple R-squared:  0.787,  Adjusted R-squared:  0.7851 
#> F-statistic: 405.3 on 3 and 329 DF,  p-value: < 2.2e-16

Confidence Interval

confint(xlm, level = LEVEL)

Example

confint(m1, level = 0.90)

#>                           5 %        95 %
#> (Intercept)       -4980.19064 -3046.16714
#> speciesChinstrap   -300.33123  -110.41973
#> speciesGentoo       127.11143   441.93578
#> flipper_length_mm    35.52645    45.68588

Model Hypothesis Testing

• Motivating Example

• Mathematical Models

• \(\beta\) Hypothesis Testing

• Model Hypothesis Testing

• Model Assumptions

Model inference

We conduct model inference to determine if different models are better at explaining variation. A common example is to compare a linear model (\(\hat Y=\hat\beta_0 + \hat\beta_1 X\)) to the mean of Y (\(\hat \mu_y\)). We determine the significance of the variation explained using an Analysis of Variance (ANOVA) table and F test.

Model Inference

Given 2 models:

\[ \hat Y = \hat\beta_0 + \hat\beta_1 X_1 + \hat\beta_2 X_2 + \cdots + \hat\beta_p X_p \]

or

\[ \hat Y = \bar y \]

Is the model with predictors do a better job than using the average?

ANOVA

ANOVA Table

Source	DF	SS	MS	F
Model	\(DFR=k-1\)	\(SSR\)	\(MSR=\frac{SSM}{DFR}\)	\(\hat F=\frac{MSR}{MSE}\)
Error	\(DFE=n-k\)	\(SSE\)	\(MSE=\frac{SSE}{DFE}\)
Total	\(TDF=n-1\)	\(TSS=SSR+SSE\)

\[ \hat F \sim F(DFR, DFE) \]

Conducting an ANOVA in R

xlm <- lm(Y ~ X, data = DATA)
summary(xlm)

Example

summary(m1)

#> 
#> Call:
#> lm(formula = body_mass_g ~ species + flipper_length_mm, data = penguins)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -898.8 -252.0  -24.8  229.8 1191.6 
#> 
#> Coefficients:
#>                   Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)       -4013.18     586.25  -6.846 3.74e-11 ***
#> speciesChinstrap   -205.38      57.57  -3.568 0.000414 ***
#> speciesGentoo       284.52      95.43   2.981 0.003083 ** 
#> flipper_length_mm    40.61       3.08  13.186  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 373.3 on 329 degrees of freedom
#> Multiple R-squared:  0.787,  Adjusted R-squared:  0.7851 
#> F-statistic: 405.3 on 3 and 329 DF,  p-value: < 2.2e-16

Model Inference

Model inference can be extended to compare models that have different number of predictors.

Model Inference

Given:

\[ M1:\ \hat y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 \]

\[ M2:\ \hat y = \beta_0 + \beta_1 X_1 \]

Let \(M1\) be the FULL (larger) model, and let \(M2\) be the RED (Reduced, smaller) model.

Model Inference

He can test the following Hypothesis:

• \(H_0\): The error variations between the FULL and RED model are not different.
• \(H_1\): The error variations between the FULL and RED model are different.

Test Statistic

\[ \hat F = \frac{[SSE(RED) - SSE(FULL)]/[DFE(RED)-DFE(FULL)]}{MSE(FULL)} \]

\[ \hat F \sim F[DFE(RED) - DFE(FULL), DFE(FULL)] \]

ANOVA in R

full <- lm(Y  ~  X1 + X2 + X3 + X4)
red <- lm(Y ~ X1 + X2)
anova(red, full)

Example

m1 <- lm(body_mass_g ~ species + island + flipper_length_mm, penguins)
m2 <- lm(body_mass_g ~ island + flipper_length_mm, penguins)
anova(m2, m1)

#> Analysis of Variance Table
#> 
#> Model 1: body_mass_g ~ island + flipper_length_mm
#> Model 2: body_mass_g ~ species + island + flipper_length_mm
#>   Res.Df      RSS Df Sum of Sq      F    Pr(>F)    
#> 1    329 47774435                                  
#> 2    327 45552857  2   2221579 7.9738 0.0004157 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model Assumptions

• Motivating Example

• Mathematical Models

• \(\beta\) Hypothesis Testing

• Model Hypothesis Testing

• Model Assumptions

Model Assumptions

When we are conducting inference linear regression, we will have to check the following conditions:

• Linearity
• Independence
• Normality
• Equal Variances
• Multicollinearity (for MLR)

Linearity

Probably considered the most important assumption, but there must be a linear relationship between both the outcome variable (y) and a set of predictors (\(x_1\), \(x_2\), …).

Independence

The data points must not influence each other.

Normality

The model errors (also known as residuals) must follow a normal distribution.

Equal Variances

The variability of the data points must be the same for all predictor values.

Residuals

Residuals are the errors between the observed value and the estimated model. Common residuals include

• Raw Residual

• Standardized Residual

• Jackknife (studentized) Residuals

Influential Measurements

Influential measures are statistics that determine how much a data point affects the model. Common influential measures are

• Leverages

• Cook’s Distance

Raw Residuals

\[ \hat r_i = y_i - \hat y_i \]

Residual Analysis

A residual analysis is used to test the assumptions of linear regression.

QQ Plot

A qq (quantile-quantile) plot will plot the estimated quantiles of the residuals against the theoretical quantiles from a normal distribution function. If the points from the qq-plot lie on the \(y=x\) line, it is said that the residuals follow a normal distribution.

Residual vs Fitted Plot

This plot allows you to assess the linearity, constant variance, and identify potential outliers. Create a scatter plot between the fitted values (x-axis) and the raw/standardized residuals (y-axis).

Variance Inflation Factor

The variance inflation factor is a measurement on how much variables are collinear with each other. A value greater than 10 is a cause for concern and action should be taken.

Residual Analysis in R

Use the resid_df function to obtain the residuals of a model.

rdf <- resid_df(LM_OBJECT)

Residual vs Fitted Plot

ggplot(RDF, aes(fitted, resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

QQ Plot

ggplot(RDF, aes(sample = resid)) + 
  stat_qq() +
  stat_qq_line() 

Example

xlm <- lm(body_mass_g ~   island + species + flipper_length_mm,
          penguins)
dfxlm <- resid_df(xlm)

ggplot(dfxlm, aes(fitted, resid)) +
  geom_point() +
  geom_hline(yintercept = 0, col = "red")

ggplot(dfxlm, aes(sample = resid)) + 
  stat_qq() +
  stat_qq_line()