Numerical Data

R Packages

  • rcistats
  • tidyverse

Palmer Penguins

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

Palmer Penguins

The penguins data set was contains information on penguins from the Palmer Station located in . You can learn more about the data set here.

An image of several penguins in Antartica.

Artwork by @allison_horst

Variables of Interest

Describing numerical data

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

What is numerical data?

Code 
penguins |> 
  slice(1:7) |> 
  pull(flipper_len)
#> [1] 181 186 195 193 190 181 195

Central Tendency

Code 
penguins |> 
  slice(1:7) |> 
  pull(flipper_len)
#> [1] 181 186 195 193 190 181 195

Variation

Code 
penguins |> 
  slice(1:7) |> 
  pull(flipper_len)
#> [1] 181 186 195 193 190 181 195

Summary Statistics

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

Summary Statistics

Summary statistics are used to describe the distribution of data.

Central Tendency

Central tendency is a statistical concept that refers to the central or typical value around which a set of data points tends to cluster. It is used to summarize and describe a data set by identifying a single representative value that provides insights into the data’s overall characteristics.

Variation

Variation in statistics refers to the extent to which data points in a dataset deviate or differ from a central tendency measure. Understanding variation is crucial for making informed decisions, drawing meaningful conclusions, and assessing the reliability of statistical analyses.

Minimum

The minimum (min) is the smallest value in the data.

Maximum

The maximum (max) is the largest value in the data.

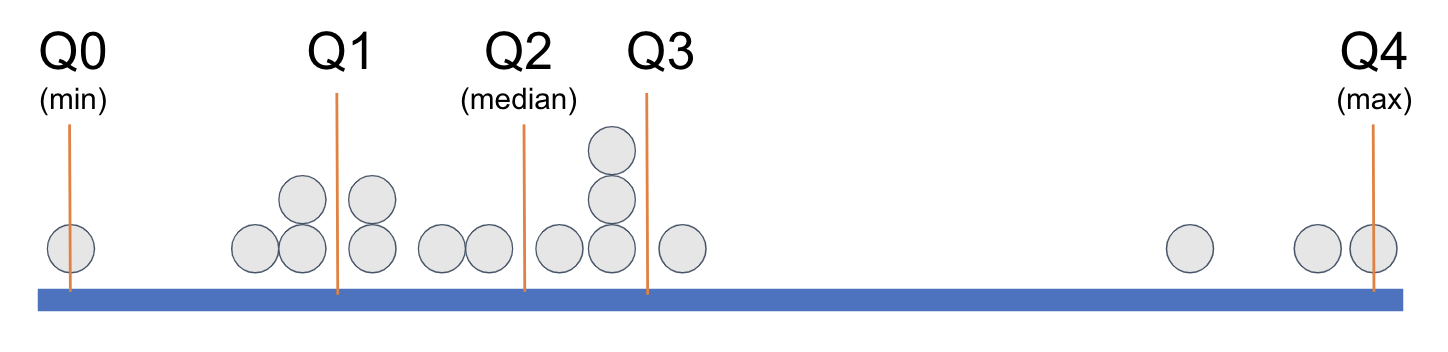
Quartiles

Quartiles are three values (Q1, Q2, Q3) that divides the data into four subsets.

Q1

Q1 is the value signifying that a quarter of the data (25%) is lower than it.

A density plot of flipper length for each penguin. The lower 25% of the of the density plot is shaded. This shading represents the location to the 25th percentile.

Q2 - Median (\(\tilde{x}\))

Q2 is the value signifying that half of the data (50%) is below it.

The median also represents the central tendency of the data.

A density plot of flipper length for each penguin. The lower 50% of the of the density plot is shaded. This shading represents the location to the 50th percentile.

Q3

Q3 is the value signifying that 3 quarters (75%) of the data is below it.

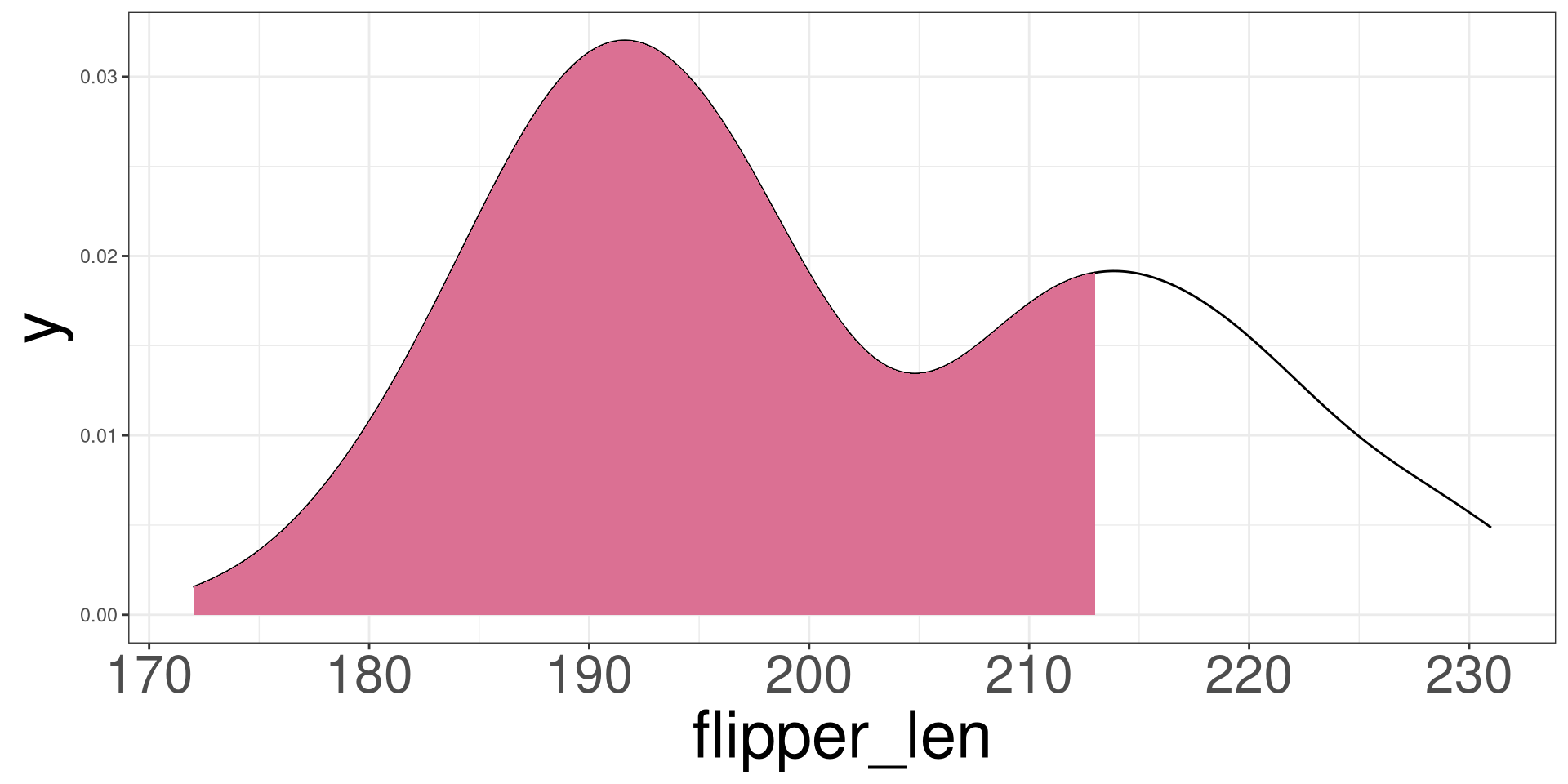
A density plot of flipper length for each penguin. The lower 75% of the of the density plot is shaded. This shading represents the location to the 75th percentile.

Interquartile Range

\[ IQR = Q_3 - Q_1 \]

A density plot of flipper length for each penguin. The middle 50% of the data is shaded. This shading represents interquartile range.

Range

\[ R = \mathrm{max} - \mathrm{min} \]

How to identify the quartiles?

  1. Sort the data
  2. ID Max and Min
  3. Find the amount of data the makes a quarter:
    1. \(K=N/4\)
  4. Create 4 groups using the sorted data
    1. group by data size
    2. If \(K\) has a decimal, the \(Kth\) value is quartile of each group.

Mean (\(\bar{x}\))

Describe how you will find the mean of these numbers:

#> [1] 18 18 12 18 13

Mean (\(\bar{x}\))

The mean is another measurement for central tendency.

\[ \bar X = \frac{1}{n}\sum^n_{i=1}X_i \]

  • \(n\): total data points

  • \(X_i\): data points

  • \(i\): indexing data

  • \(\sum\): add all from first (bottom) to last (up)

Variance

The variance is a measurement on the average squared distance the data points are from the central tendency.

\[ s^2 = \frac{1}{n-1}\sum^n_{i=1}(X_i-\bar X)^2 \]

Standard Deviation

The standard deviation is a measurement on the average distance the data points are from the central tendency.

\[ s=\sqrt{s^2} \]

Mean vs Median

Mean

\[ \bar X = \frac{1}{n}\sum^n_{i=1}x_i \]

Median

\[ P(X \leq \tilde{X}) = 0.5 \]

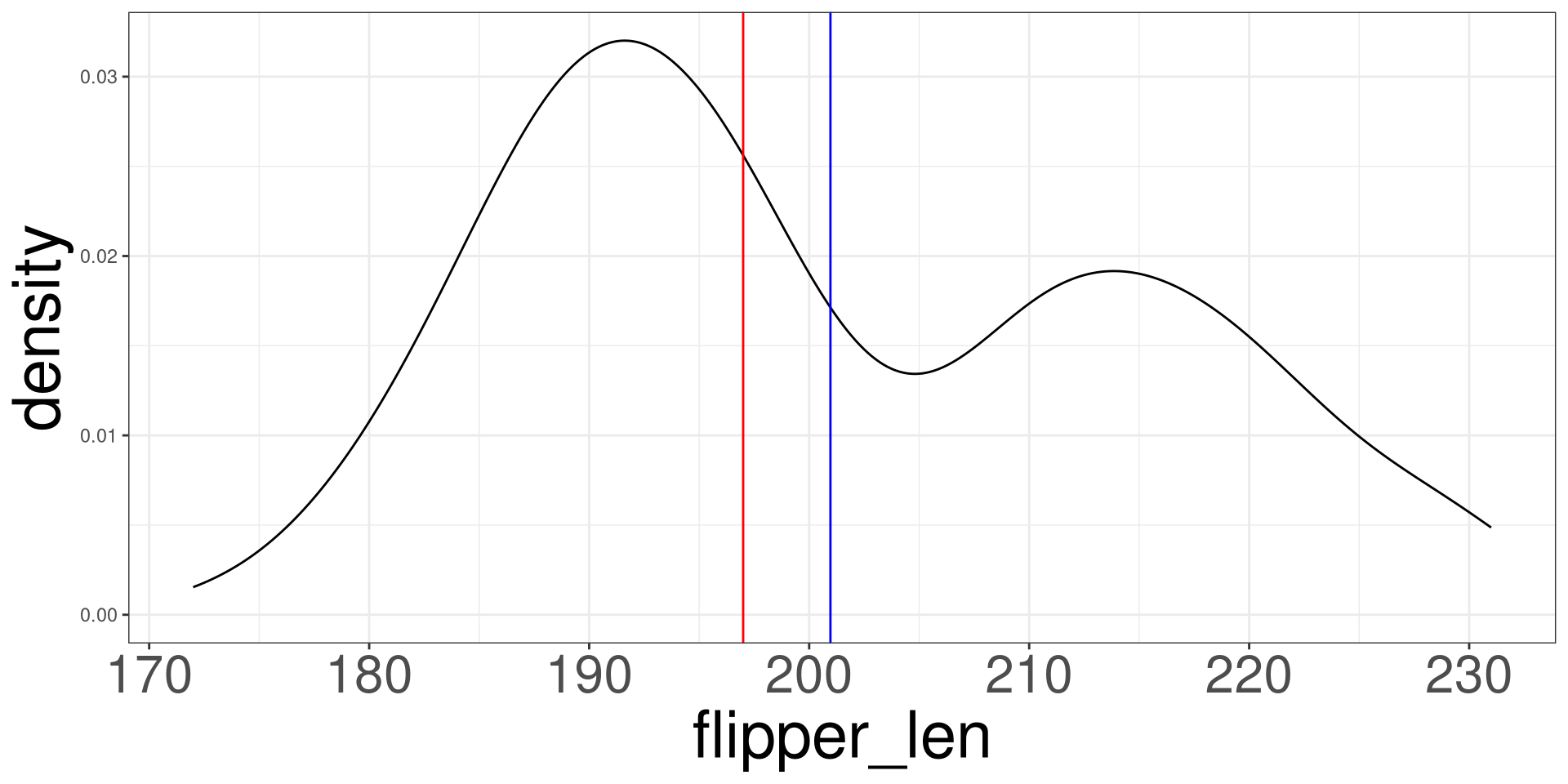
Mean vs Median

Mean (blue line) vs Median (red line)

A density plot of flipper length for each penguin. The mean and median are repsesented as vertical lines. The mean is located at approximately 201. The median is located at approximately 197.

Outliers

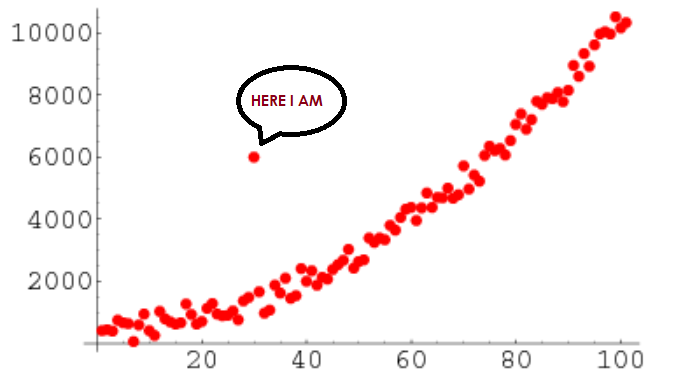
These are data points that seem to be highly distant from all other variables.

An image of a scatter plot with the points following an exponential curve. One point is far from the curve.

Numerical Statistics in R

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

Numerical Statistics in R

R has several built in functions to compute statistics.

Mean

mean(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Median

median(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Standard Deviation

sd(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Variance

var(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Quartiles

quantile(DATA$VAR, probs = c(0.25, 0.5, 0.75))
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Max and Min

max(DATA$VAR)
min(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Summary Statistics

rnum_stats(DATA$VAR)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Penguins

Code 
num_stats(penguins$flipper_len)
#>   min q25    mean median q75 max     sd     var iqr missing
#> 1 172 190 200.967    197 213 231 14.016 196.442  23       0

Data Visualization

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

Histogram

A histogram is a graphical representation of the distribution or frequency of data points in a dataset. It provides a visual way to understand the shape, central tendency, and spread of a dataset by dividing the data into intervals or bins and showing how many data points fall into each bin as a bar.

Histogram R Code

ggplot(DATA, aes(VAR)) +
  geom_histogram()

To change bins:

ggplot(DATA, aes(VAR)) +
  geom_histogram(bins = VAL)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)
  • VAL: Numerical value to change the bin width.

Histogram

Code 
y <- rnorm(1000)
ggplot(tibble(y), aes(y)) +
  geom_histogram(bins = 15)

Histogram

Code 
y <- rgamma(1000, 2)
ggplot(tibble(y), aes(y)) +
  geom_histogram(bins = 15)

Histograms

Code 
y <- rbeta(1000, 5, 1)
ggplot(tibble(y), aes(y)) +
  geom_histogram(bins = 15)

Histograms

Code 
y <- rbinom(1000, 1, 0.4)
z <- (y == 0) * rnorm(1000, 23) + (y == 1) * rnorm(1000, 27)
ggplot(tibble(z), aes(z)) +
  geom_histogram(bins = 15)

Penguins

ggplot(penguins, aes(flipper_len)) +
  geom_histogram()

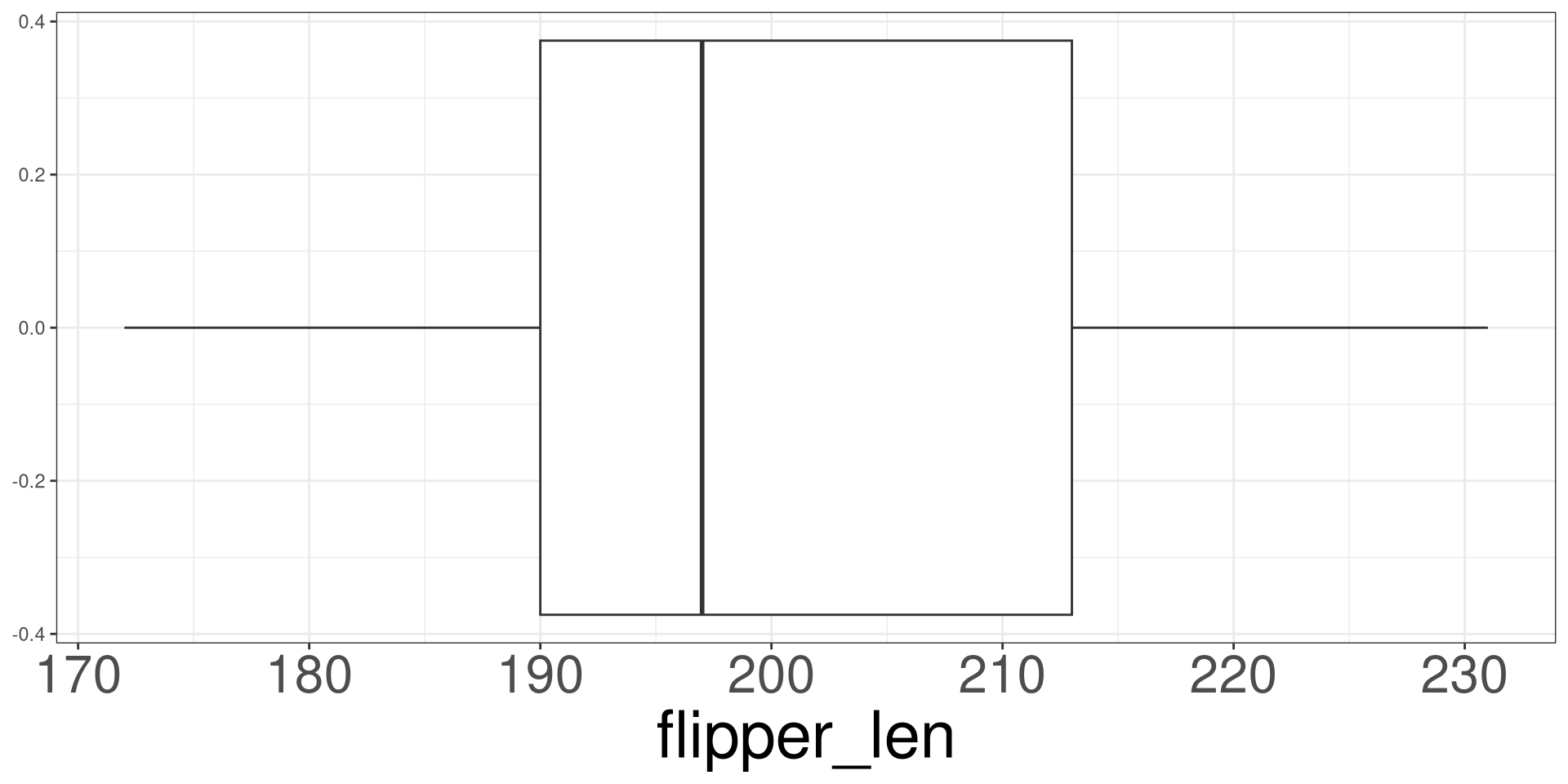
Box Plot

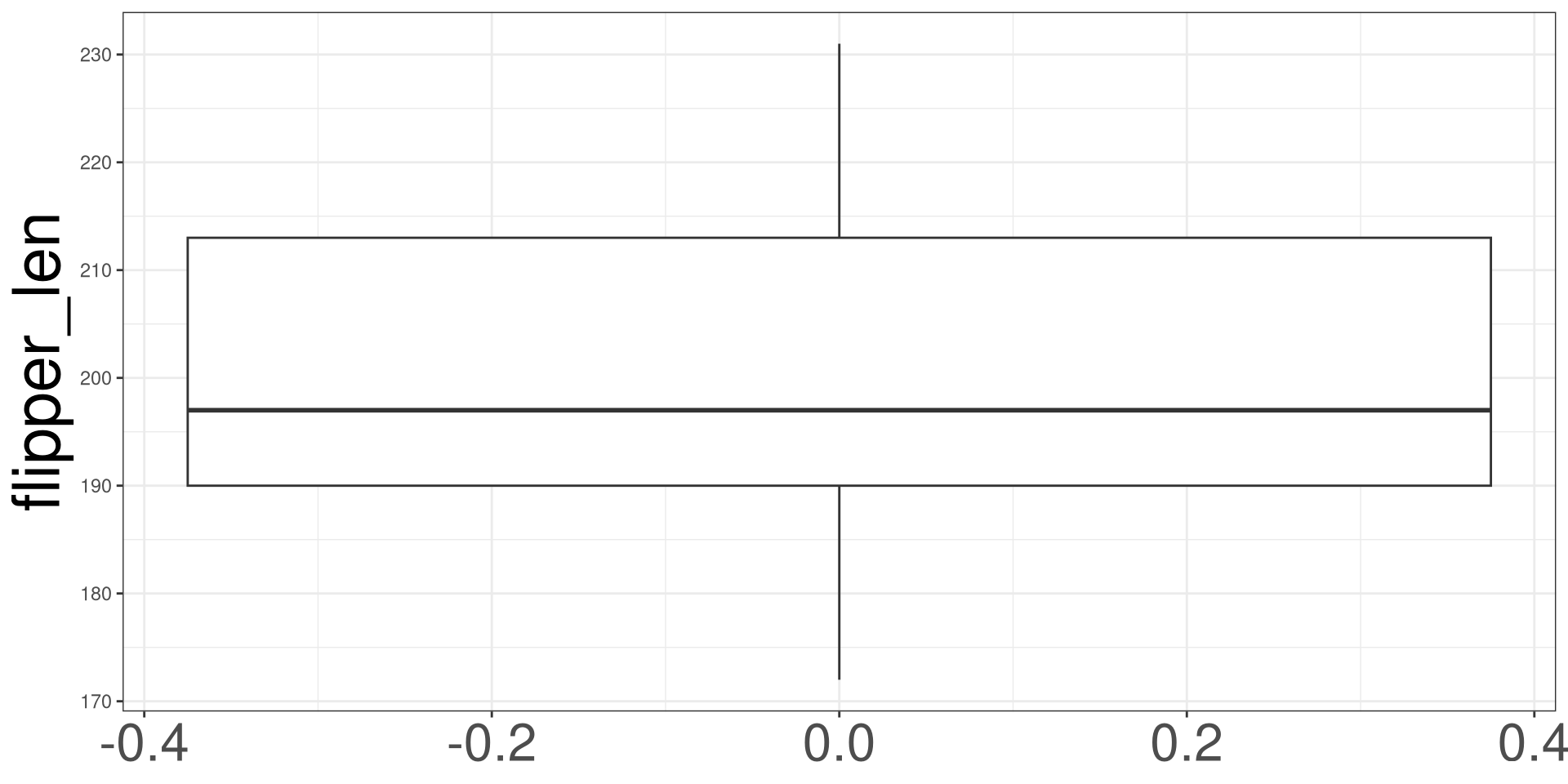
A box plot, also known as a box-and-whisker plot, is a graphical representation of the distribution and key statistical characteristics of a dataset. It provides a visual summary of the data’s central tendency, spread, and potential outliers.

Box Plot

Box Plot R Code

ggplot(DATA, aes(VAR)) +
  geom_boxplot()
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Box Plot

ggplot(penguins, aes(flipper_len)) +
  geom_boxplot()

Box Plot

ggplot(penguins, aes(y = flipper_len)) +
  geom_boxplot()

Dot Plots

Dot Plots are similar to histograms, but they incorporate dots to count how many data points fall within bins.

Dot Plots in R

ggplot(DATA, aes(VAR)) +
  geom_dotplot()

To change binwidth

ggplot(DATA, aes(VAR)) +
  geom_dotplot(binwidth = VAL)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)
  • VAL: Numerical value to change the bin width.

Dot Plots

ggplot(penguins, aes(flipper_len)) +
  geom_dotplot(binwidth = 1)

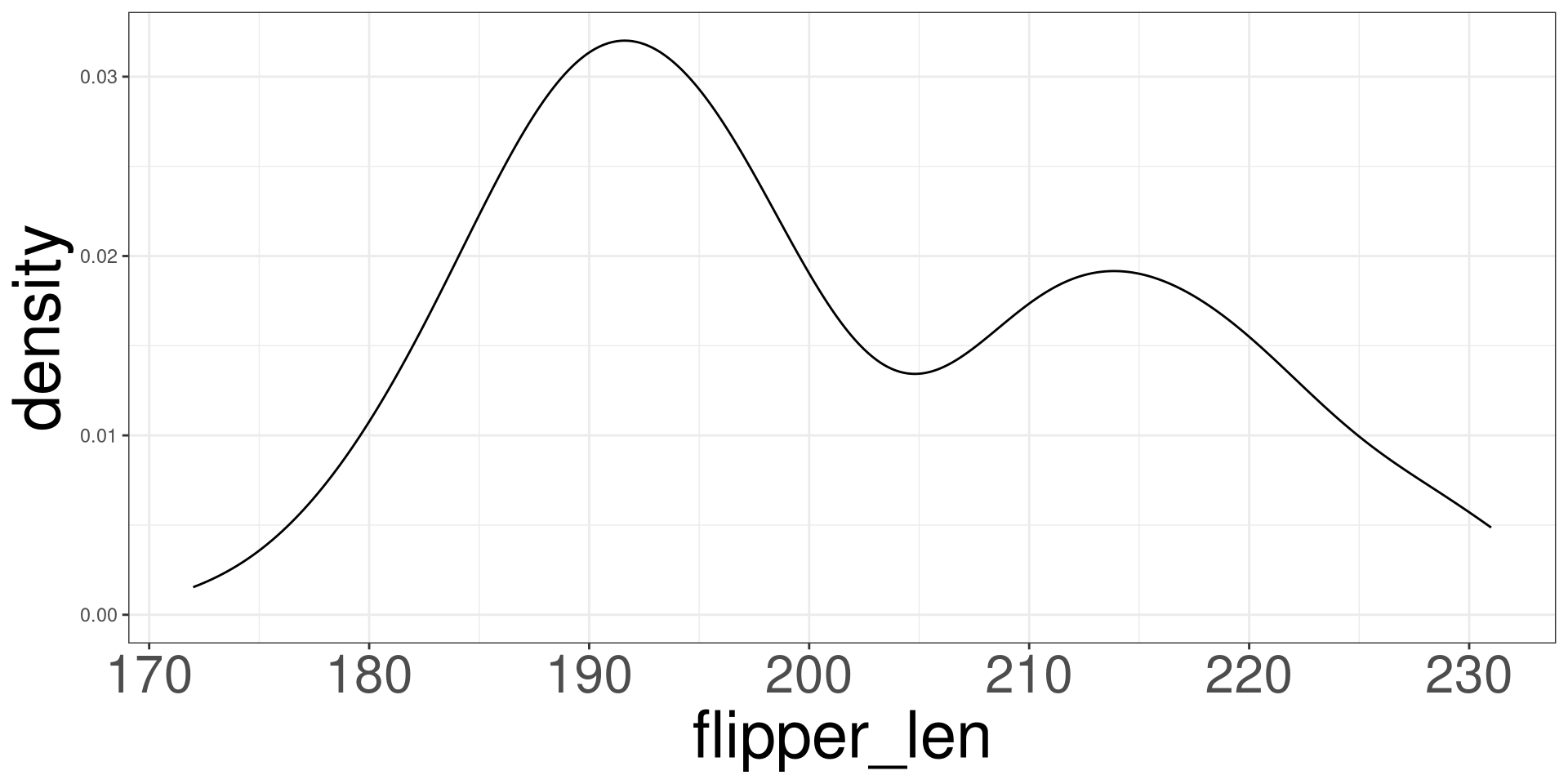
Density Plot

Density Plot

A density plot is a way to visualize the distribution of a continuous variable — it shows where data values are concentrated (dense) and where they are sparse via the height of the graph.

Density Plot in R

ggplot(DATA, aes(VAR)) +
  geom_density()
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)

Density Plot

ggplot(penguins, aes(flipper_len)) +
  geom_density()

Adding Vertical Lines

ggplot(DATA, aes(VAR)) +
  geom_density() +
  geom_vline(xintercept = XVAL)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)
  • XVAL: Number to place the vertical line (eg: 5)

Vertical Lines

ggplot(penguins, aes(flipper_len)) +
  geom_density() +
  geom_vline(xintercept = mean(penguins$flipper_len), col  = "blue") +
  geom_vline(xintercept = median(penguins$flipper_len), col = "red")

Adding Horizontal Lines

ggplot(DATA, aes(VAR)) +
  geom_density() +
  geom_hline(yintercept = YVAL)
  • DATA: Name of the data frame (eg: penguins)
  • VAR: Name of the variable to create a plot (eg: flipper_len)
  • YVAL: Number to place the horizontal line (eg: 2)

Horizontal Lines

ggplot(penguins, aes(flipper_len)) +
  geom_density() +
  geom_hline(yintercept = 0.01, col  = "blue") +
  geom_hline(yintercept = 0.02, col = "red")

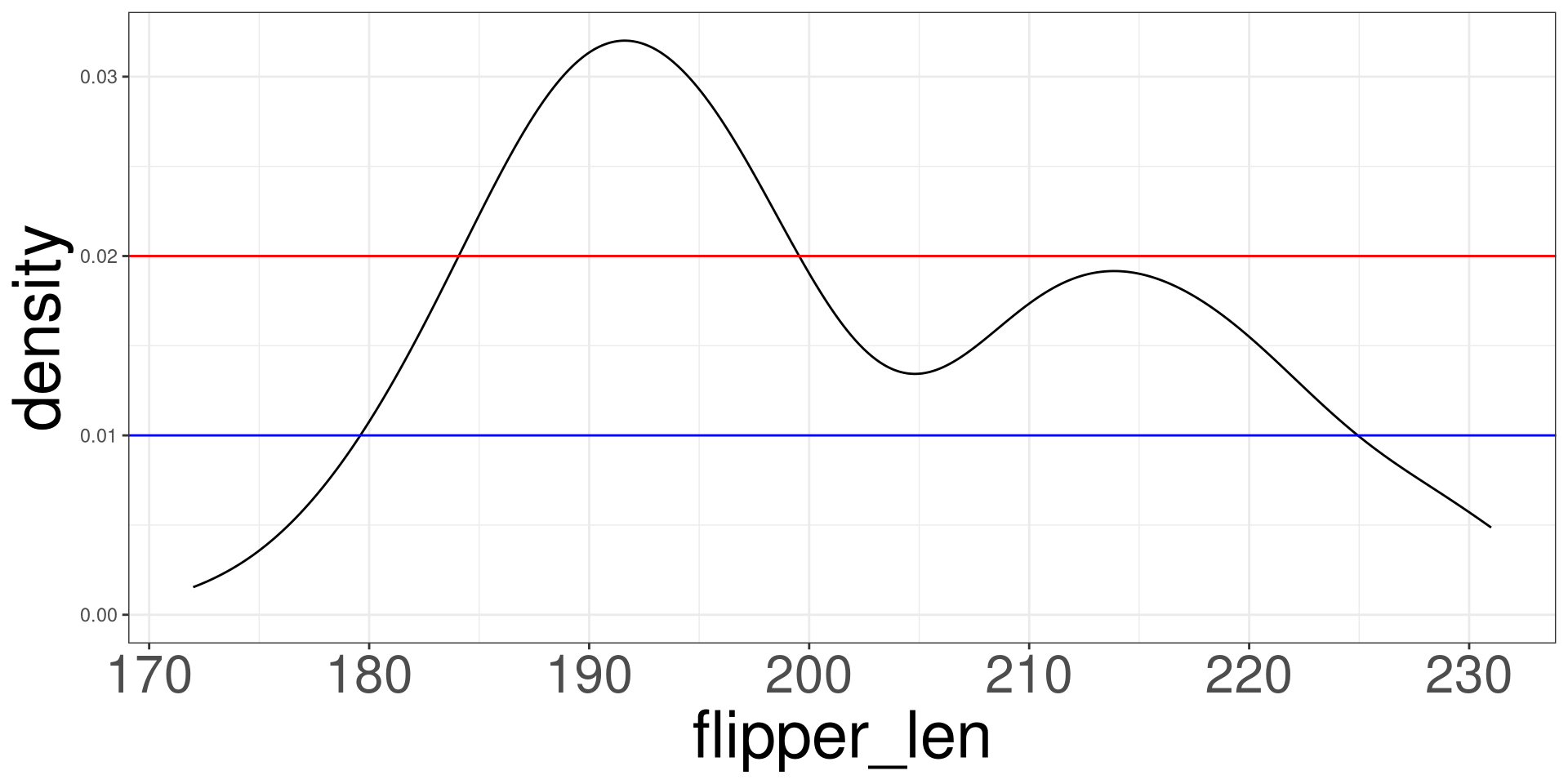
Skeweness

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

Skeweness

Skewness is a statistical measure to determine if unimodal data follows a symmetric distribution, skewed to the left, or skewed to the right.

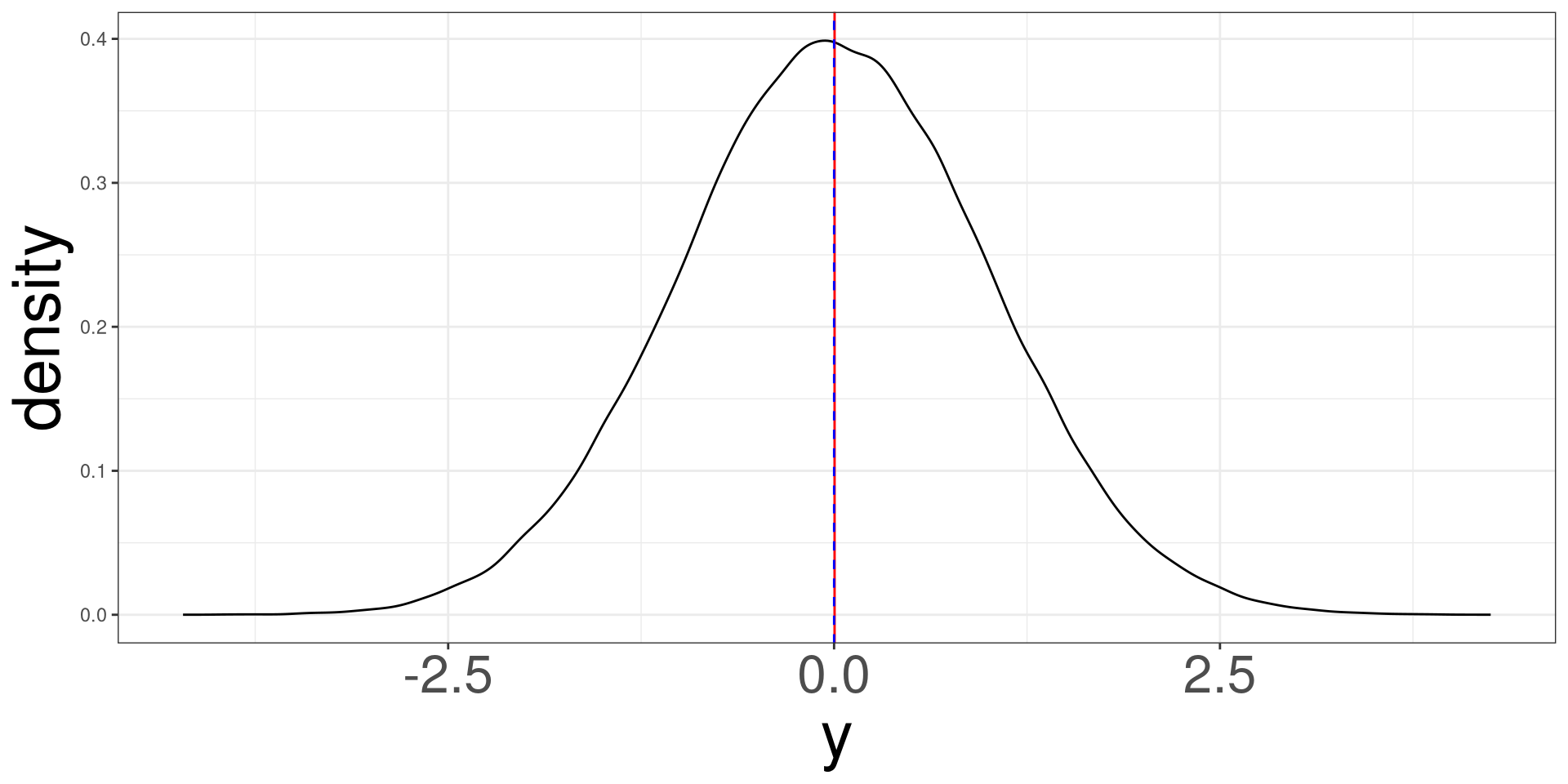
Symmetric Distribution

A symmetric distribution will look bell shaped and the mean (red line) and median (dashed blue line) will overlap each other.

Code 
y <- rnorm(100000)
ggplot(tibble(y), aes(y)) +
  geom_density() +
  geom_vline(xintercept = mean(y), col = "red") +
  geom_vline(xintercept = median(y), col = "blue", lty = 2)
A bell shaped curve where the mean and the median are represented as lines and overlap each other.

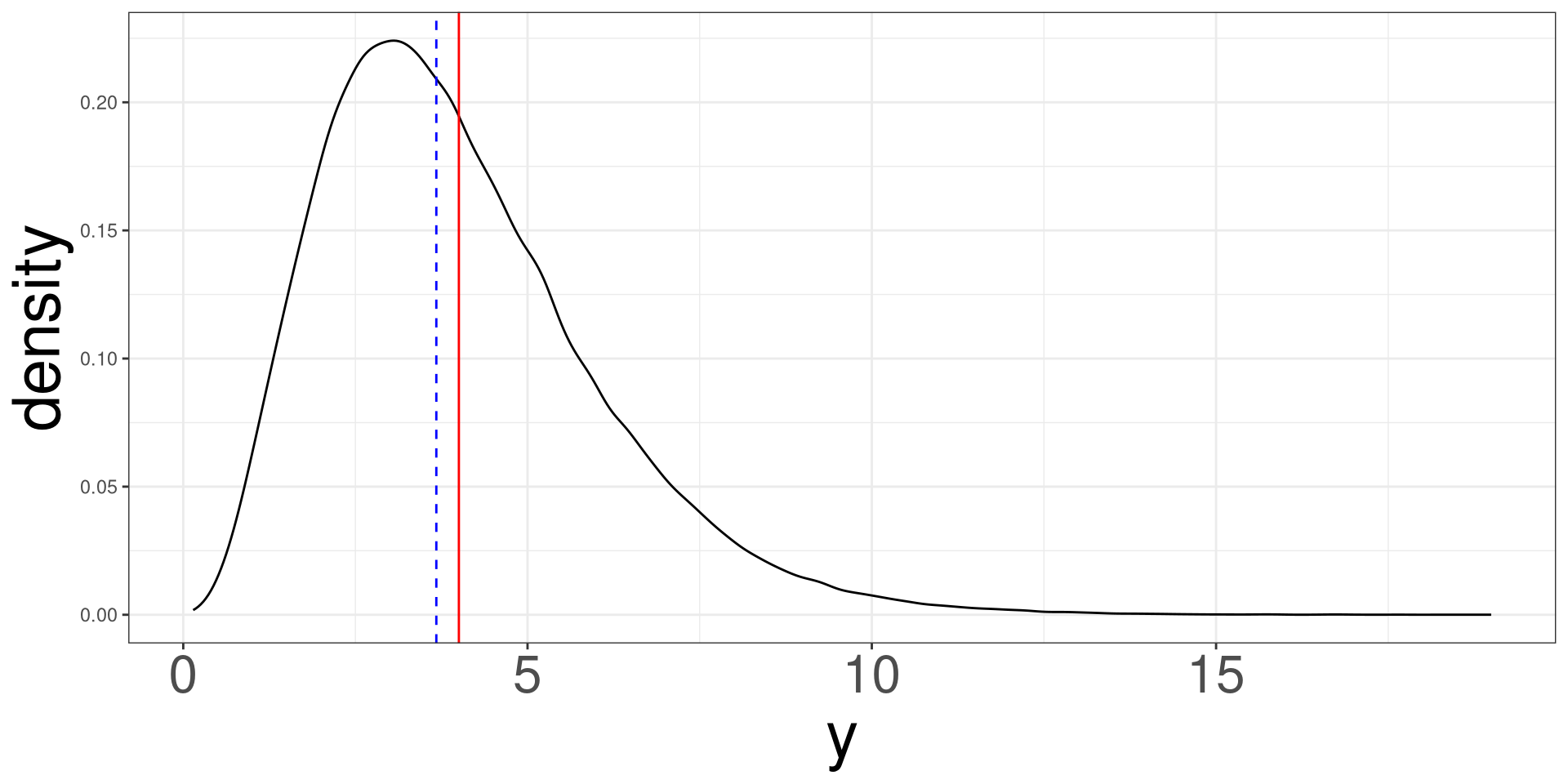
Right Skewed Distribution

A right skewed distribution looks asymetric and the mean (red line) is to the right of the median (dashed blue line).

Code 
y <- rgamma(100000, shape = 4)
ggplot(tibble(y), aes(y)) +
  geom_density() +
  geom_vline(xintercept = mean(y), col = "red") +
  geom_vline(xintercept = median(y), col = "blue", lty = 2)
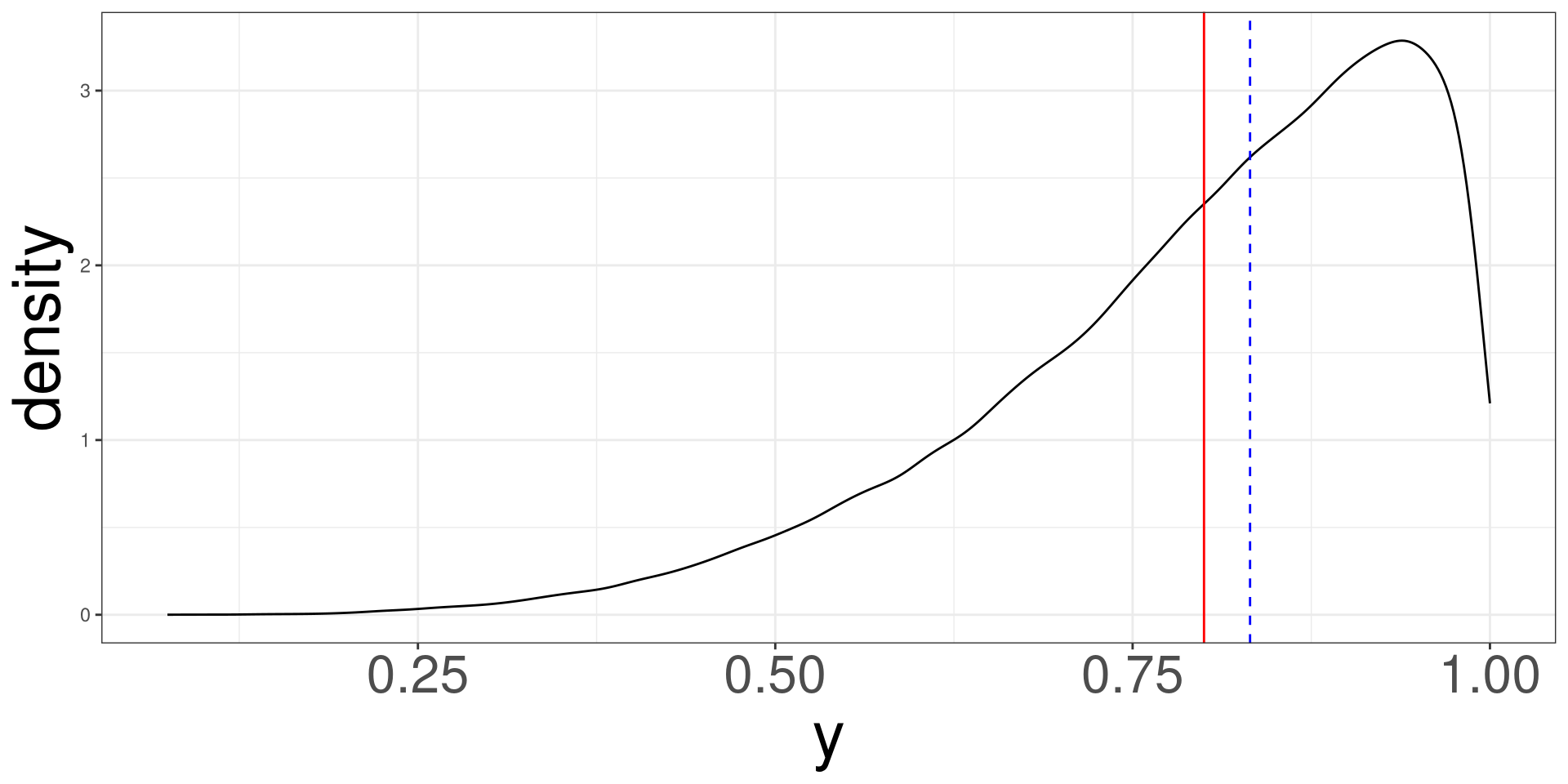
A bell shaped curve where the mean and the median are represented as lines and overlap each other.

left Skewed Distribution

A left skewed distribution looks asymetric and the mean (red line) is to the left of the median (dashed blue line).

Code 
y <- rbeta(100000, shape1 = 5, shape2 = 1.25)
ggplot(tibble(y), aes(y)) +
  geom_density() +
  geom_vline(xintercept = mean(y), col = "red") +
  geom_vline(xintercept = median(y), col = "blue", lty = 2)
A bell shaped curve where the mean and the median are represented as lines and overlap each other.

Scatter Plots

  • Palmer Penguins

  • Describing numerical data

  • Summary Statistics

  • Numerical Statistics in R

  • Data Visualization

  • Skeweness

  • Scatter Plots

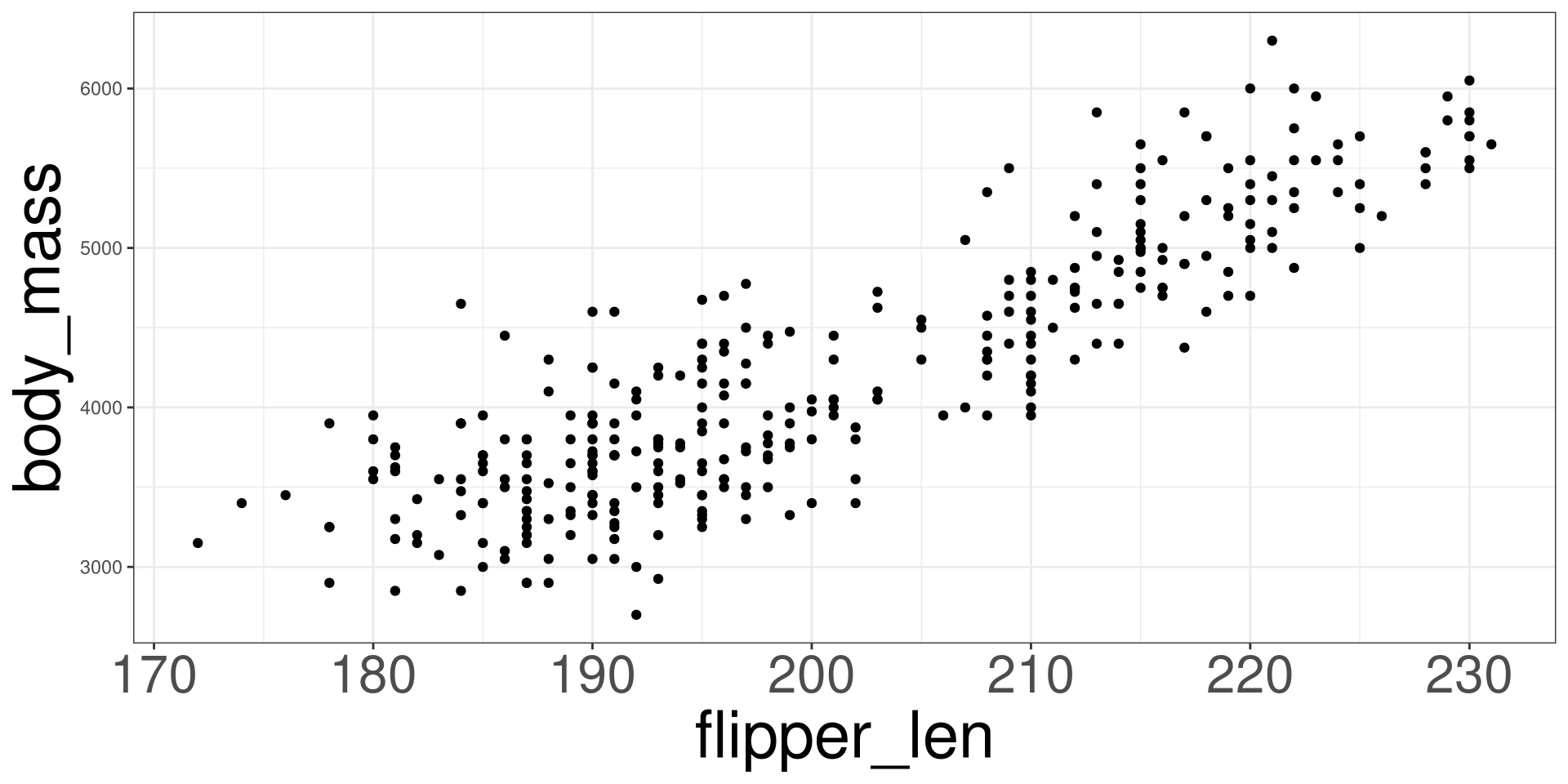
Scatter Plots

Scatter plots demonstrate how two variables behave with each other. They can tell you any postive or negative trends, if they exist, with the combination of the plots.

Positive Relationship

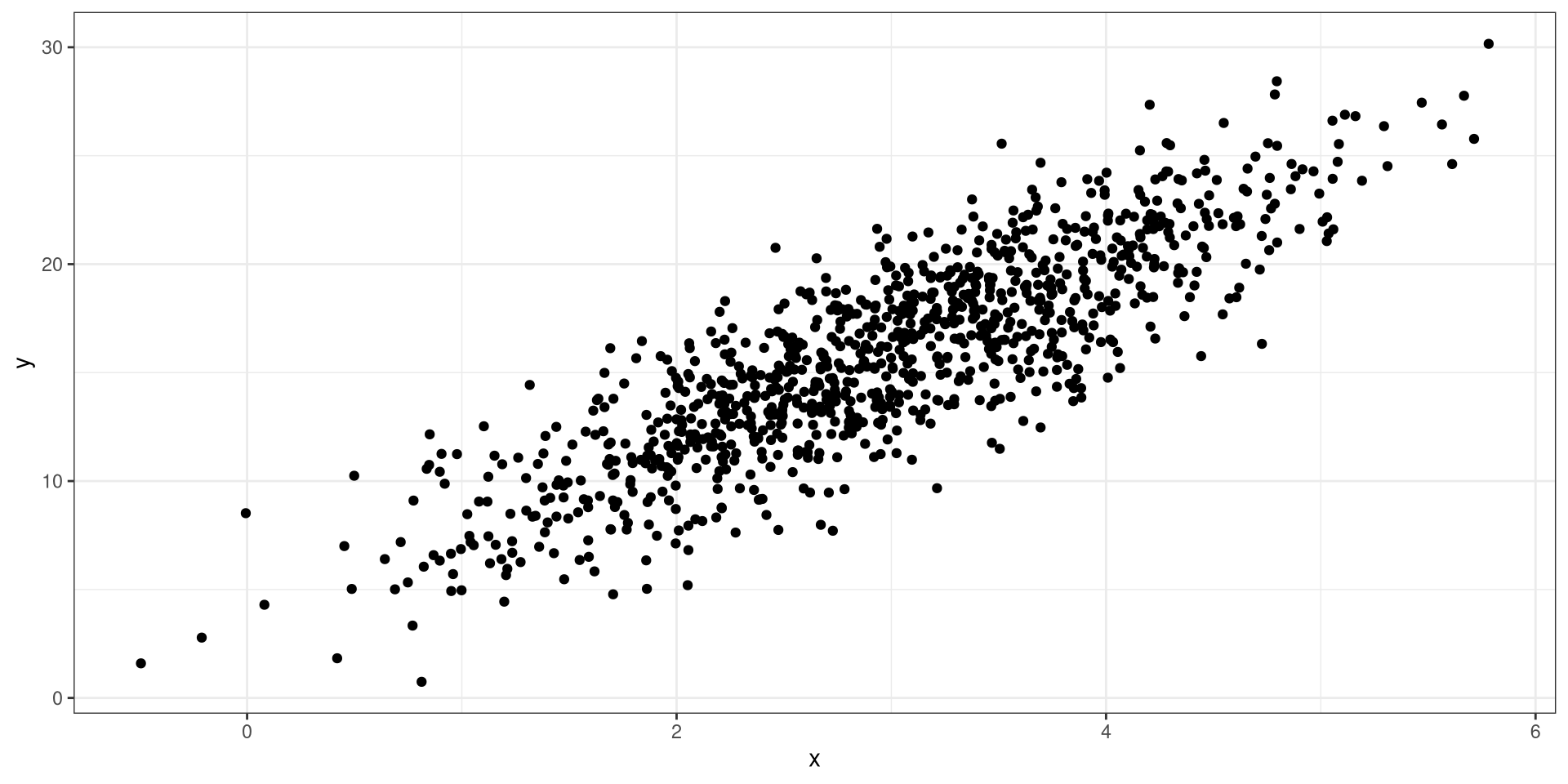
Negative Relationship

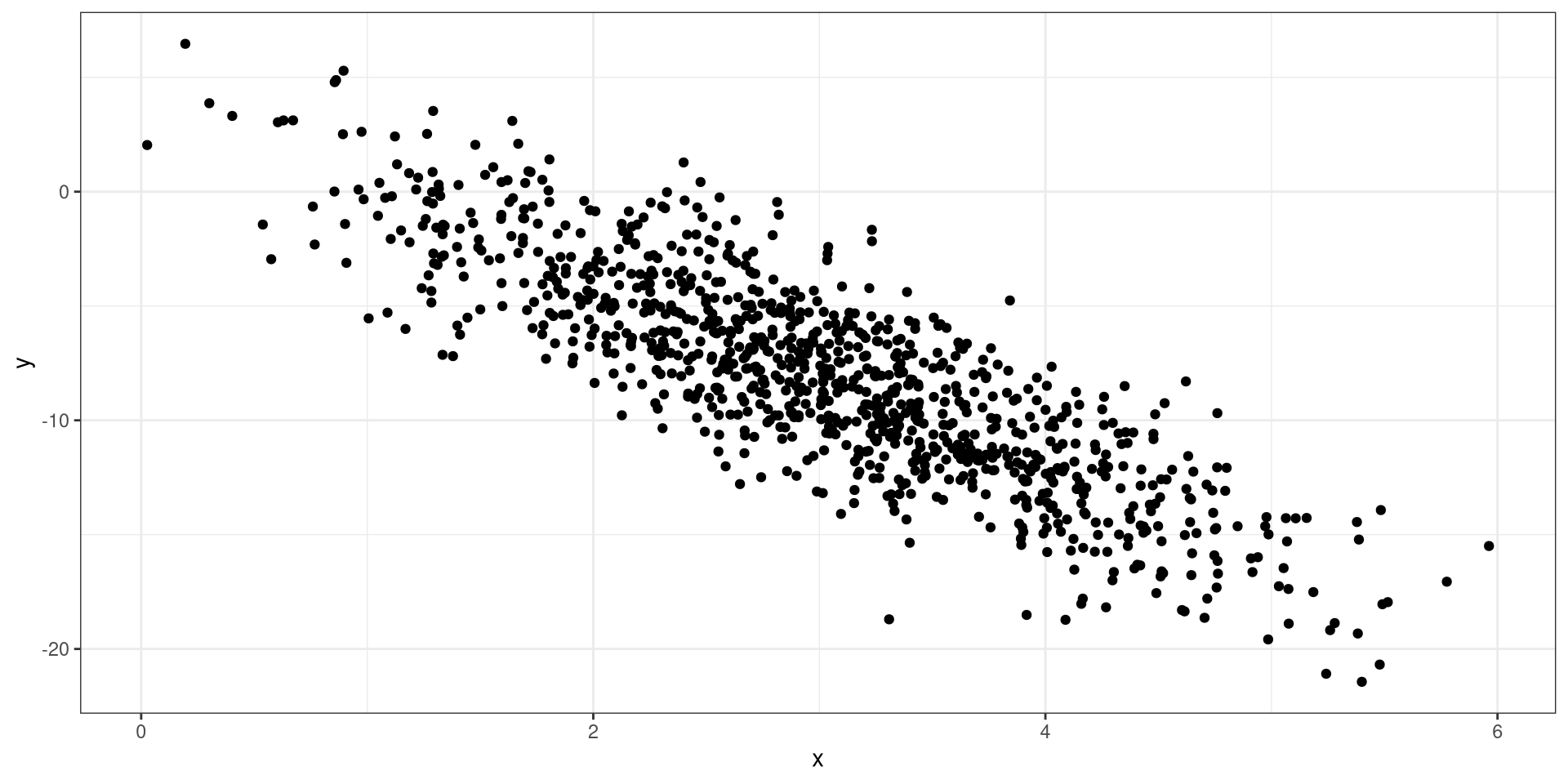
No Relationship

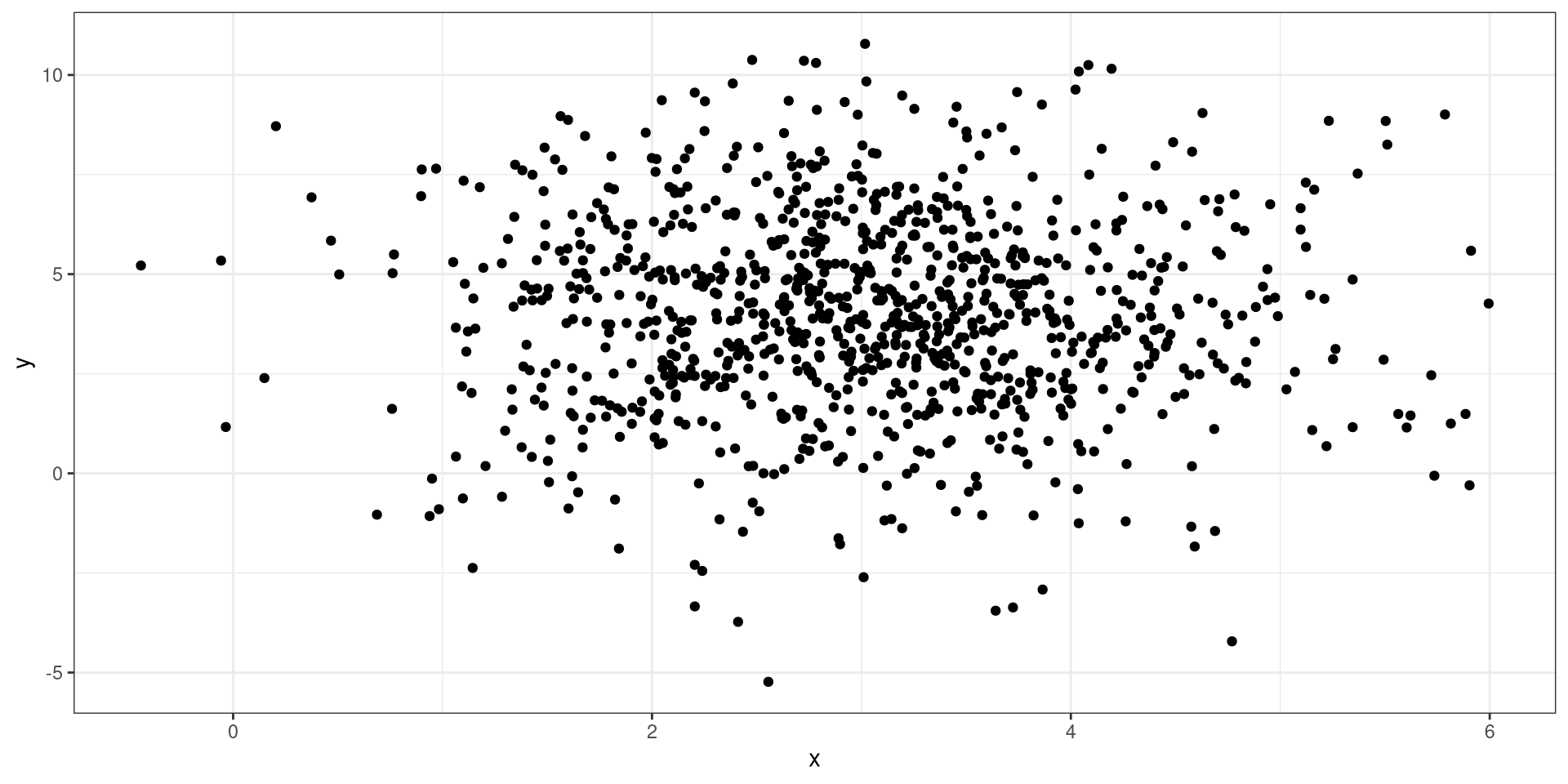
Weak Relationship

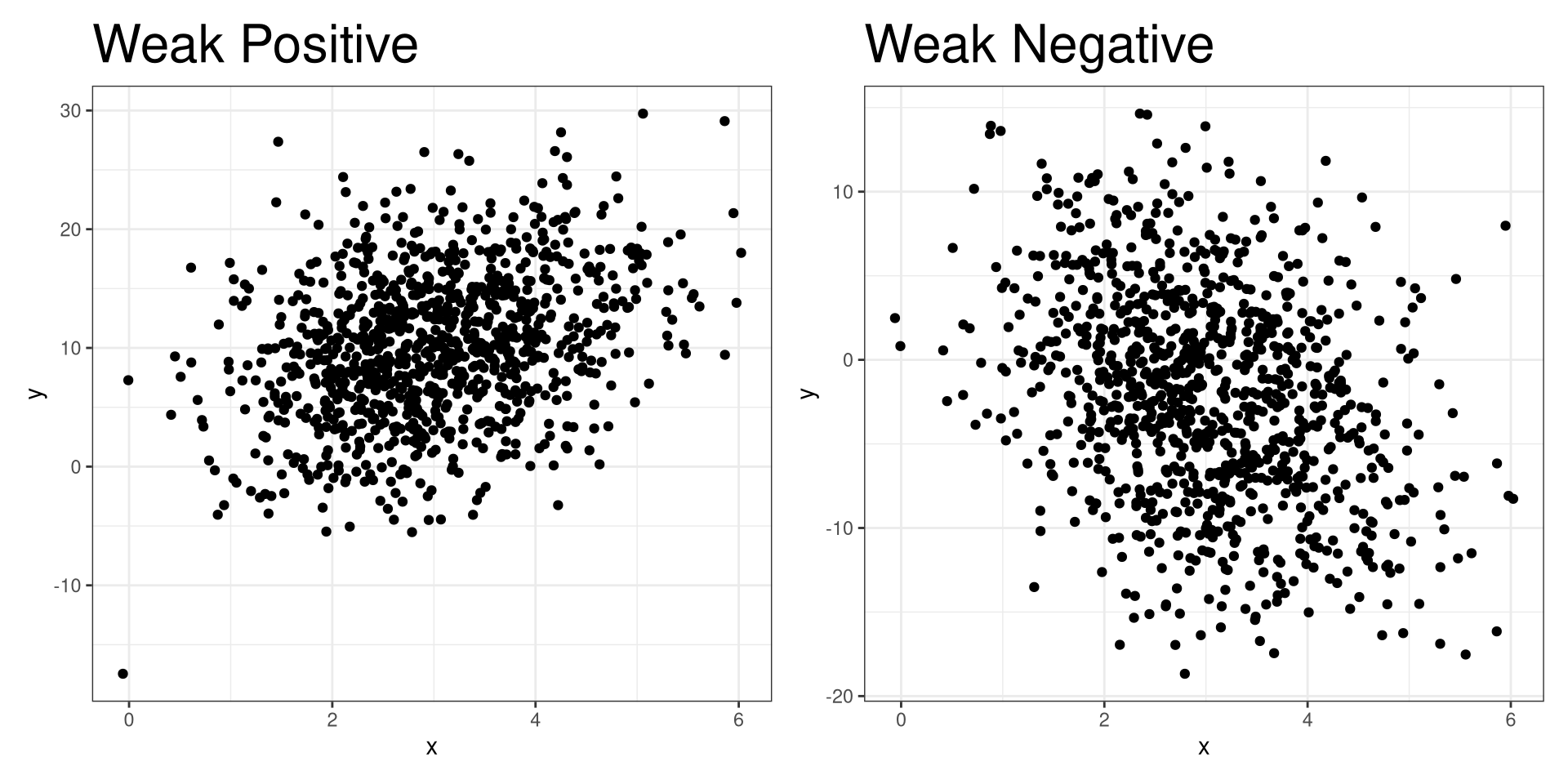
Scatter Plots in R

ggplot(DATA, aes(x = VAR1, y = VAR2)) +
  geom_point()
  • DATA: Name of the data frame (eg: penguins)
  • VAR1: Name of the X variable to create a plot (eg: flipper_len)
  • VAR2: Name of the Y variable to create a plot (eg: body_mass)

Penguins

Code 
ggplot(penguins, aes(flipper_len, body_mass)) +
  geom_point()