Group
Regression

R Packages

  • rcistats
  • tidyverse

Palmer Penguins Data

Variables of Interest

  • species: Penguin species
  • body_mass: Body mass in grams

An image of several penguins in Antartica.

Artwork by @allison_horst

Heart Disease Data

Variables of Interest

  • thal: Thallium stress test result
  • disease: Indicating if they have heart disease

An image of a graph and a heart.

Modeling Relationships

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

Explaining Continuous Variables

Code 
ggplot(penguins, aes(body_mass)) +
  geom_density()

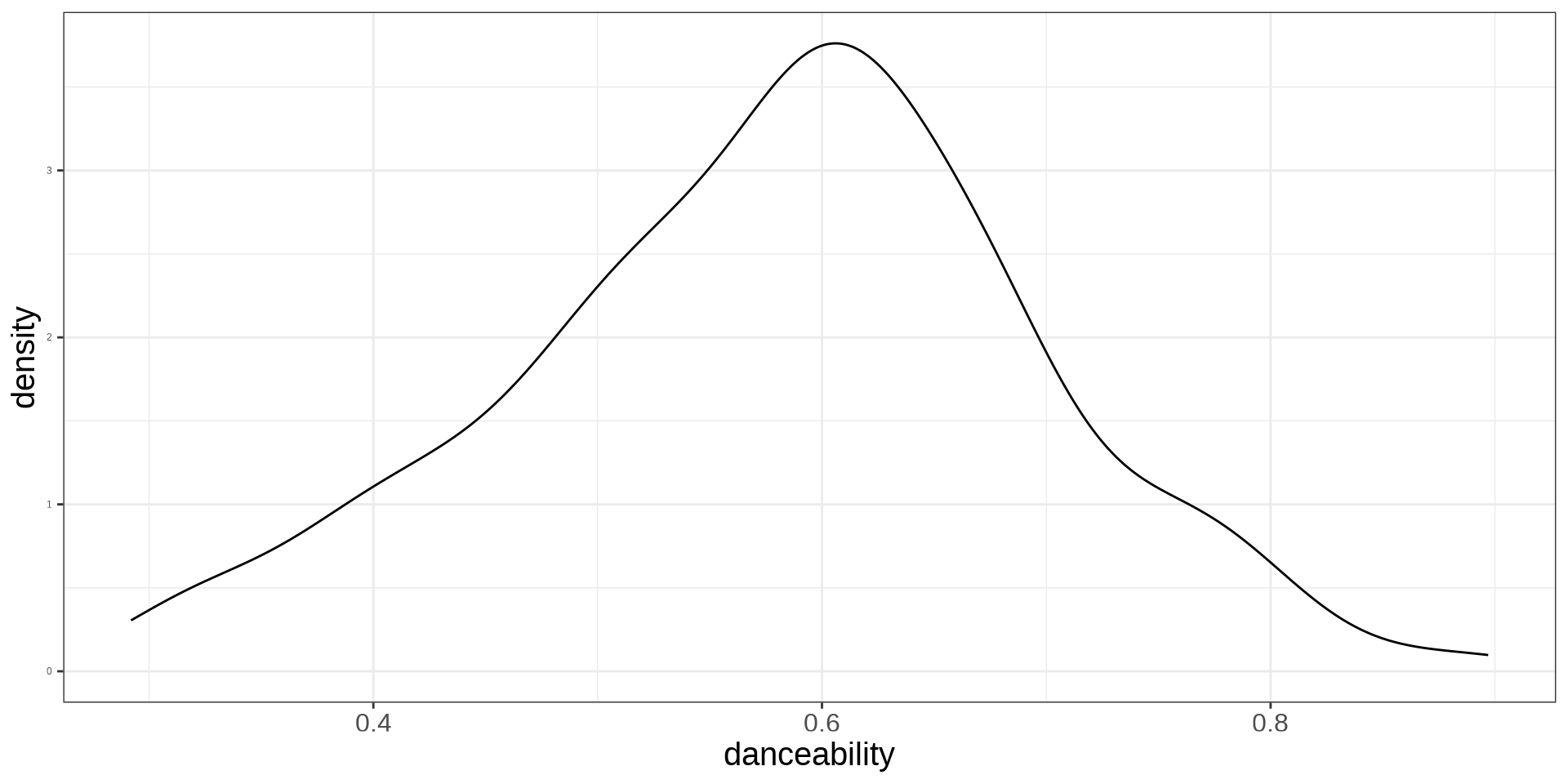
Linear: Categorical Variables

Code 
ggplot(penguins, aes(body_mass, fill = species)) +
  geom_density(alpha = .5)

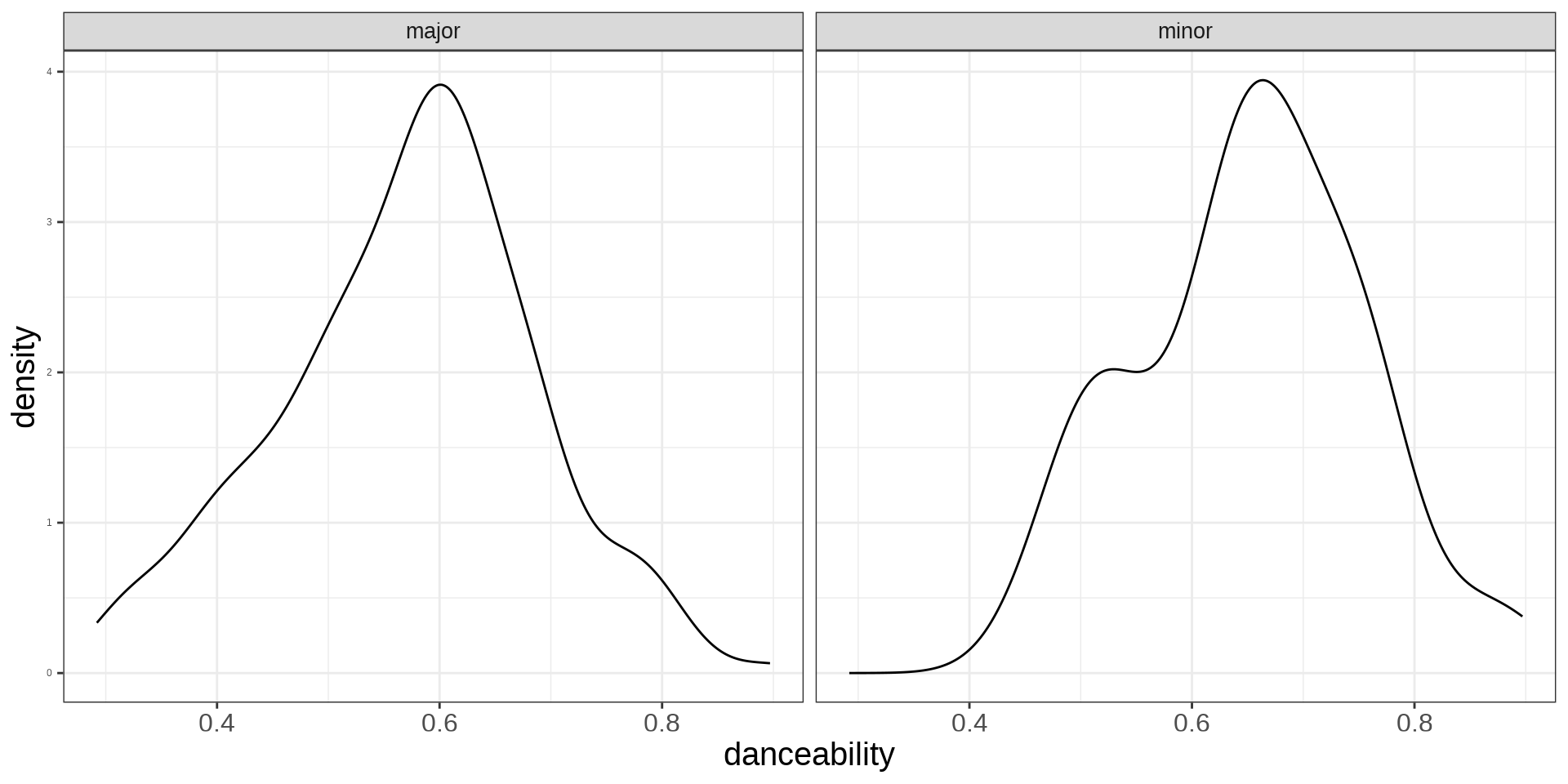
Explainging Binary Variables

Code 
heart_disease |> 
  ggplot(aes(disease)) +
  geom_bar()

Logistic: Categorical Variables

Code 
heart_disease |> 
  ggplot(aes(disease, fill = thal)) +
  geom_bar()

Group Statistics

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

Group Statistics

We can use statistics to explain a variable by the categories.

Compute statistics for each group.

Continuous Data

num_by_cat_stats(DATA, NUM, CAT)
  • NUM: Name of the numerical variable
  • CAT: Name of the categorical variable
  • DATA: Name of the data frame

Continous Data

num_by_cat_stats(penguins, body_mass, species)
#>   Categories  min    q25     mean median  q75  max      sd      var   iqr
#> 1     Adelie 2850 3362.5 3706.164   3700 4000 4775 458.620 210332.4 637.5
#> 2  Chinstrap 2700 3487.5 3733.088   3700 3950 4800 384.335 147713.5 462.5
#> 3     Gentoo 3950 4700.0 5092.437   5050 5500 6300 501.476 251478.3 800.0
#>   missing
#> 1       0
#> 2       0
#> 3       0

Continuous Data

cat_stats(DATA$Y, DATA$X, prop = "row")

OR

cat_stats(DATA$X, DATA$Y, prop = "col")
  • Y: Name of the outcome variable
  • X: Name of the categorical variable
  • DATA: Name of the data frame

Binary Data

cat_stats(heart_disease$disease, heart_disease$thal, prop = "row")
#> $frequency
#>      
#>       Normal Fixed Defect Reversible Defect
#>   no     127            6                27
#>   yes     37           12                88
#> 
#> $row_prop
#>      
#>       Normal Fixed Defect Reversible Defect
#>   no  0.7938       0.0375            0.1688
#>   yes 0.2701       0.0876            0.6423

Group Models

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

G/LM with Categorical Variables

A line is normally used to model 2 continuous variables.

However, the predictor variable \(X\) can be restricted to a set a dummy variables that can symbolize categories.

A category from \(X\) will be used as a reference for a model.

LM Example

\[ body\_mass = \beta_0 + \boldsymbol \beta (species) \]

\[ body\_mass = \beta_0 + \beta_1 (Chinstrap) + \beta_2 (Gentoo) \]

\(Chinstrap\) and \(Gentoo\) are both dummy variables that will reference Adelie

GLM Example

\[ lo(disease) = \beta_0 + \boldsymbol \beta (thal) \]

\[ lo(disease) = \beta_0 + \beta_1 (Fixed) + \beta_2 (Reversible) \]

\(Fixed\) and \(Reversible\) defects are both dummy variables that will reference Normal

Dummy Variables

To fit a model with categorical variables, we must utilize dummy (binary) variables that indicate which category is being referenced. We use \(C-1\) dummy variables where \(C\) indicates the number of categories. When coded correctly, each category will be represented by a combination of dummy variables.

Dummy Variables

Binary variables are variable that can only take on the value 0 or 1.

\[ D_i = \left\{ \begin{array}{cc} 1 & Category\\ 0 & Other \end{array} \right. \]

Example

If we have 4 categories, we will need 3 dummy variables:

Cat 1 Cat 2 Cat 3 Cat 4
Dummy 1 1 0 0 0
Dummy 2 0 1 0 0
Dummy 2 0 0 1 0

Species Dummy Variables

DUMMY Chinstrap Gentoo Adelie (Reference)
\(Chinstrap\) 1 0 0
\(Gentoo\) 0 1 0

Thal Dummy Variables

DUMMY Fixed Defect Reversible Defect Normal (Reference)
\(Fixed\) 1 0 0
\(Reversible\) 0 1 0

LM: Penguins

\[ body\_mass = \hat \beta_0 + \hat\beta_1 (Chinstrap) + \hat\beta_2 (Gentoo) \]

\(\hat \beta_1\) indicates how body mass changes from Adelie to Chinstrap.

\(\hat \beta_2\) indicates how body mass changes from Adelie to Gentoo.

\(\hat \beta_0\) represents the baseline level, in this case the body mass of Adelie.

GLM: Penguins

\[ lo(disease) = \hat \beta_0 + \hat\beta_1 (Fixed) + \hat\beta_2 (Reversible) \]

\(\hat \beta_1\) indicates how \(lo(disease)\) changes from Normal to Fixed.

\(\hat \beta_2\) indicates how \(lo(disease)\) changes from Normal to Reversible.

\(\hat \beta_0\) represents the baseline level, in this case the \(lo(disease)\) of Normal.

Interepreting \(\beta\)

Interpreting \(\beta\) for categorical variables are different from continuous (numeric) variables. Interpreting \(\beta\)s only allow us to make comparisons between the dummy indicator category and the reference category

LM: Interpreting \(\beta\)

\[ \hat Y = \hat \beta_0 + \hat\beta_1 D \]

\[ D = \left\{ \begin{array}{cc} 1 & CAT\\ 0 & REF \end{array} \right. \]

On average, CAT1 has a larger/smaller Y than REF by about \(\beta_1\).

GLM: Interpreting \(\beta\)

\[ lo(Y) = \hat \beta_0 + \hat\beta_1 D \]

\[ D = \left\{ \begin{array}{cc} 1 & CAT\\ 0 & REF \end{array} \right. \]

The odds of having Y is \(e^{\beta_1}\) times higher/lower for CAT than Ref.

Group Models in R

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

Fitting an LM in R

xlm <- lm(Y ~ X, data = DATA)
xlm
  • X: Name Predictor Variable of Interest in data frame DATA, must be a factor variable
  • Y: Name Outcome Variable of Interest in data frame DATA
  • DATA: Name of the data frame

Fitting an GLM in R

xglm <- glm(Y ~ X, data = DATA, family = binomial())
xglm
  • X: Name Predictor Variable of Interest in data frame DATA, must be a factor variable
  • Y: Name Outcome Variable of Interest in data frame DATA
  • DATA: Name of the data frame

X not a Factor

xlm <- lm(Y ~ factor(X), data = DATA)

OR

xglm <- glm(Y ~ factor(X), data = DATA, family = binomial())
  • X: Name Predictor Variable of Interest in data frame DATA, not a factor variable
  • Y: Name Outcome Variable of Interest in data frame DATA
  • DATA: Name of the data frame

LM Example

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

Example

xlm <- lm(body_mass ~ species, penguins)
xlm
#> 
#> Call:
#> lm(formula = body_mass ~ species, data = penguins)
#> 
#> Coefficients:
#>      (Intercept)  speciesChinstrap     speciesGentoo  
#>          3706.16             26.92           1386.27

\[ \hat Y_i = 3706 + 26.92 (Chinstrap) + 1386.27 (Gentoo) \]

Intepreting \(\hat \beta_1\)

On average, Chinstrap has a larger mass than Adelie by about 26.92 grams.

Intepreting \(\hat \beta_2\)

On average, Gentoo has a larger mass than Adelie by about 1386.27 grams.

Finding the Adelie MASS

\[ \hat Y_i = 3706 + 26.92 (0) + 1386.27 (0) \]

Finding the Chinstrap MASS

\[ \hat Y_i = 3706 + 26.92 (1) + 1386.27 (0) \]

Finding the Gentoo MASS

\[ \hat Y_i = 3706 + 26.92 (0) + 1386.27 (1) \]

Prediction in R

xlm <- lm(body_mass ~ species,
            data = penguins)
predict_df <- data.frame(species = "Gentoo")
predict(xlm,
        predict_df)
#>        1 
#> 5092.437
xlm <- lm(body_mass ~ species,
            data = penguins)
predict_df <- data.frame(species = "Chinstrap")
predict(xlm,
        predict_df)
#>        1 
#> 3733.088
xlm <- lm(body_mass ~ species,
            data = penguins)
predict_df <- data.frame(species = "Adelie")
predict(xlm,
        predict_df)
#>        1 
#> 3706.164

GLM Example

  • Modeling Relationships

  • Group Statistics

  • Group Models

  • Group Models in R

  • LM Example

  • GLM Example

Example

xglm <- glm(disease ~ thal, 
            data = heart_disease, 
            family = binomial())
xglm
#> 
#> Call:  glm(formula = disease ~ thal, family = binomial(), data = heart_disease)
#> 
#> Coefficients:
#>           (Intercept)       thalFixed Defect  thalReversible Defect  
#>                -1.233                  1.926                  2.415  
#> 
#> Degrees of Freedom: 296 Total (i.e. Null);  294 Residual
#> Null Deviance:       409.9 
#> Residual Deviance: 323.4     AIC: 329.4

\[ lo(disease) = -1.233 + 1.926 (Fixed) + 2.415 (Reversible) \]

Intepreting \(\hat \beta_1\)

Code 
exp(1.926)
#> [1] 6.862007

The odds of having heart disease is 6.86 times higher for a patient who has a fixed defect than a patient who is normal.

Intepreting \(\hat \beta_2\)

Code 
exp(2.415)
#> [1] 11.18977

The odds of having heart disease is 11.19 times higher for a patient who has a reversible defect than a patient who is normal.

Prediction in R

xglm <- glm(disease ~ thal, data = heart_disease,
            family = binomial())
pdf <- data.frame(thal = "Fixed Defect")
predict(xglm, pdf, type = "response")
#>         1 
#> 0.6666667
xglm <- glm(disease ~ thal, data = heart_disease,
            family = binomial())
pdf <- data.frame(thal = "Reversible Defect")
predict(xglm, pdf, type = "response")
#>         1 
#> 0.7652174
xglm <- glm(disease ~ thal, data = heart_disease,
            family = binomial())
pdf <- data.frame(thal = "Normal")
predict(xglm, pdf, type = "response")
#>         1 
#> 0.2256098