---
title: "Logistic Regression Models"
description: |
The logistic regression model, interpreting coefficients (odds & odds ratios), fitting
models in R, and predicting probabilities.
format:
html:
toc: true
toc-depth: 3
number-sections: true
code-tools: true
code-fold: false
smooth-scroll: true
editor: source
image: img/logistic.png
execute:
echo: true
warning: false
message: false
error: true
jupyter: r
knitr:
opts_chunk:
comment: "#>"
---
```{r}
#| label: setup
#| include: false
library(tidyverse)
library(rcistats)
library(MASS)
# Outcome: 1 = died from Melanoma, 0 = did not
Melanoma$dead <- ifelse(Melanoma$status == 1, 1, 0)
```
# Google Colab
Copy the following code and put it in a code cell in Google Colab. Only do this if you are using a completely new notebook.
```r
# This code will load the R packages we will use
install.packages(c("rcistats"),
repos = c("https://inqs909.r-universe.dev",
"https://cloud.r-project.org"))
library(tidyverse)
library(csucistats)
library(MASS)
# Uncomment and run for themes
# csucistats::install_themes()
# library(ThemePark)
# library(ggthemes)
# Outcome: 1 = died from Melanoma, 0 = did not
Melanoma$dead <- ifelse(Melanoma$status == 1, 1, 0)
```
# Data
## Melanoma
Melanoma is a type of skin cancer arising from melanin‑producing cells. It is dangerous because it can metastasize to other parts of the body.
## Outcome of interest
We want to understand **how predictors affect survival** during a study period. We therefore code a **binary outcome** `dead`.
## Data
We use `MASS::Melanoma` with:- `dead` (1 = died of Melanoma, 0 = otherwise),- `sex` (1 = male, 0 = female),- `age` (years),- `thickness` (tumour thickness in mm),- `ulcer` (1 = present, 0 = absent).
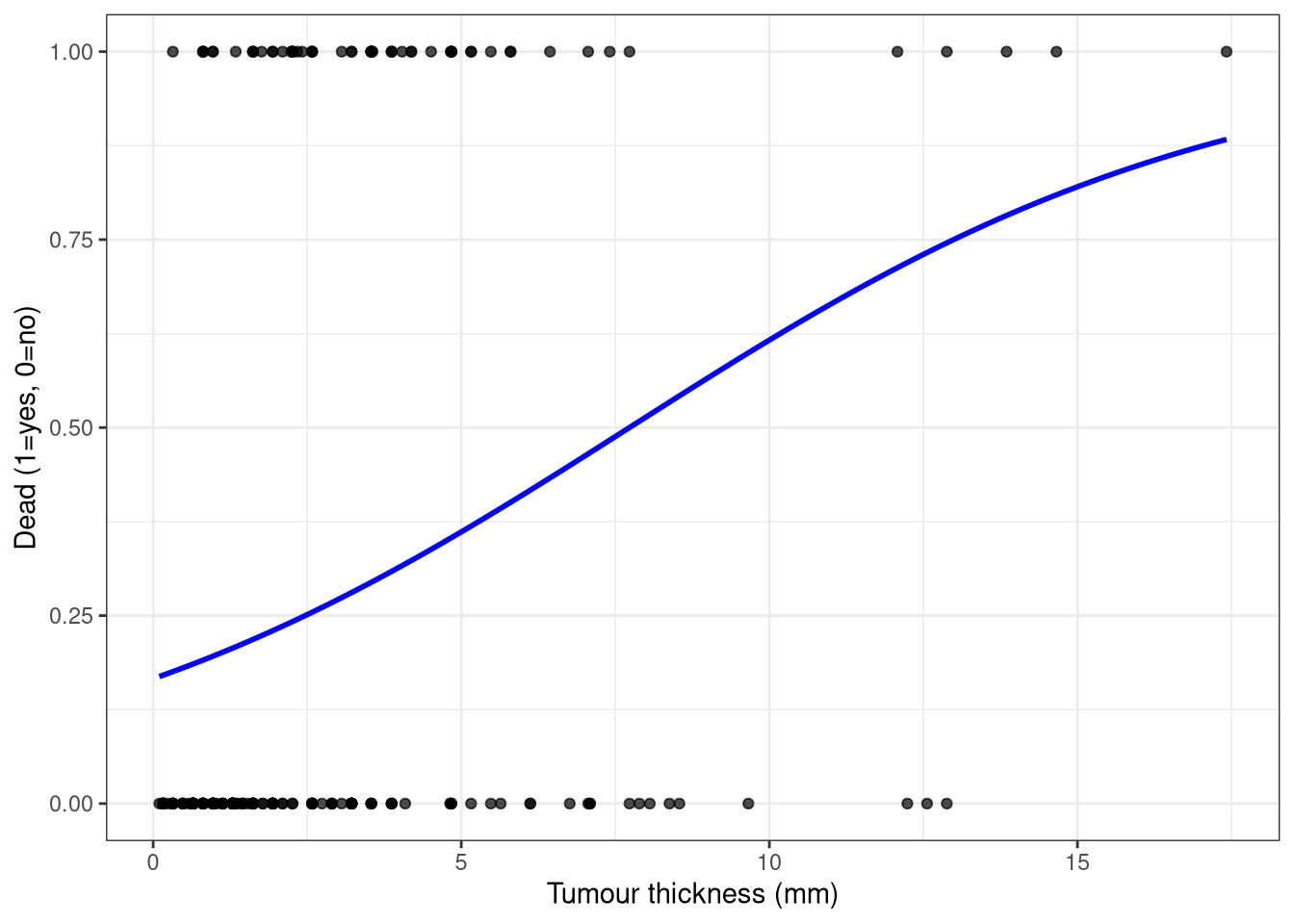
## Plot
```{r}
#| code-fold: true
ggplot(Melanoma, aes(thickness, dead)) +
geom_point(alpha = 0.7) +
labs(x = "Tumour thickness (mm)", y = "Dead (1=yes, 0=no)") +
stat_smooth(method = "glm",
se = F,
method.args = list(family = "binomial"),
color = "blue") +
theme_bw()
```
# Logistic regression in R
**Logistic regression** models the relationship between predictors and a **binary** outcome by making the **log‑odds** a linear function of the predictors.
## Fitting Model
**Template:**
```r
# Logistic regression (binomial GLM)
glm(Y ~ X1 + X2 + ... + Xp,
data = DATA,
family = binomial())
```
**Example (Melanoma):**
Model `dead` by `sex`, `age`, `thickness`, and `ulcer`:
```{r}
glm(dead ~ sex + age + thickness + ulcer,
data = Melanoma,
family = binomial())
```
The fitted logit equation can be written generically as
## Odds ratios (exponentiated coefficients)
**Template:**
```r
# Logistic regression (binomial GLM)
m <- glm(Y ~ X1 + X2 + ... + Xp,
data = DATA,
family = binomial())
exp(coef(m))
```
**Example:**
```{r}
m <- glm(dead ~ sex + age + thickness + ulcer,
data = Melanoma,
family = binomial())
exp(coef(m))
```
# Prediction with models
## Model
$$
\hat P(Y=1) = \frac{e^{\hat\beta_0 + \hat\beta_1 X_1 + \cdots + \hat\beta_p X_p}}{1 + e^{\hat\beta_0 + \hat\beta_1 X_1 + \cdots + \hat\beta_p X_p}}.
$$
**Template:**
```r
xglm <- glm(Y ~ X1 + X2 + ... + Xp,
data = DATA,
family = binomial())
new_df <- data.frame(X1 = VAL1, X2 = VAL2, ..., Xp = VALp)
predict(xglm, newdata = new_df, type = "response") # probabilities
```
**Examples (Melanoma):**
0) **Fit a model with gender, age, thickness, and ulcer present**
```{r}
xglm <- glm(dead ~ sex + age + thickness + ulcer,
data = Melanoma,
family = binomial())
```
1) **Male, age 75, thickness 2.9, ulcer present**
```{r}
new1 <- data.frame(sex = 1, age = 75, thickness = 2.9, ulcer = 1)
predict(xglm, new1, type = "response")
```
2) **Male, age 75, thickness 2.9, ulcer absent**
```{r}
new2 <- data.frame(sex = 1, age = 75, thickness = 2.9, ulcer = 0)
predict(xglm, new2, type = "response")
```
3) **Female, thickness 2.9, ulcer present — compare ages 55 vs 75**
```{r}
new3 <- tibble(sex = 0, age = c(55, 75), thickness = 2.9, ulcer = 1)
pred3 <- predict(xglm, new3, type = "response")
tibble(age = new3$age, probability = scales::percent(pred3, accuracy = 0.1))
```
# Appendix: quick reference (copy‑paste)
## Simple Logistic Regression
```r
# Fit
glm(Y ~ X, data = DATA, family = binomial())
```
- **`DATA`** → your data frame (e.g., `Melanoma`)
- **`Y`** → the outcome variable (e.g., `dead`)
- **`X`** → predictor variables (e.g `thickness`)
## Logistic Regression
```r
# Fit
glm(Y ~ X1 + X2 + ... + Xp, data = DATA, family = binomial())
```
- **`DATA`** → your data frame (e.g., `Melanoma`)
- **`Y`** → the outcome variable (e.g., `dead`)
- **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `age`, `thickness`)
## Odds Ratio
```r
m <- glm(Y ~ X1 + X2 + ... + Xp, data = DATA, family = binomial())
# Odds Ratio
exp(coef(m))
```
- **`DATA`** → your data frame (e.g., `Melanoma`)
- **`Y`** → the outcome variable (e.g., `dead`)
- **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `age`, `thickness`)
## Predict Probabilities
```r
m <- glm(Y ~ X1 + X2 + ... + Xp, data = DATA, family = binomial())
# Predict probabilities
new_df <- data.frame(X1 = VAL1, X2 = VAL2, ..., Xp = VALp)
predict(m, newdata = new_df, type = "response")
```
- **`DATA`** → your data frame (e.g., `Melanoma`)
- **`Y`** → the outcome variable (e.g., `dead`)
- **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `age`, `thickness`)
- **`VAL1`, `VAL2`, ..., `VALp`** → predictor values (e.g `55`, `2.8`)