Linear Regression Models

Explaining variation, simple & multiple linear models, categorical predictors, correlation, and prediction

1 Setup

1.1 Google Colab

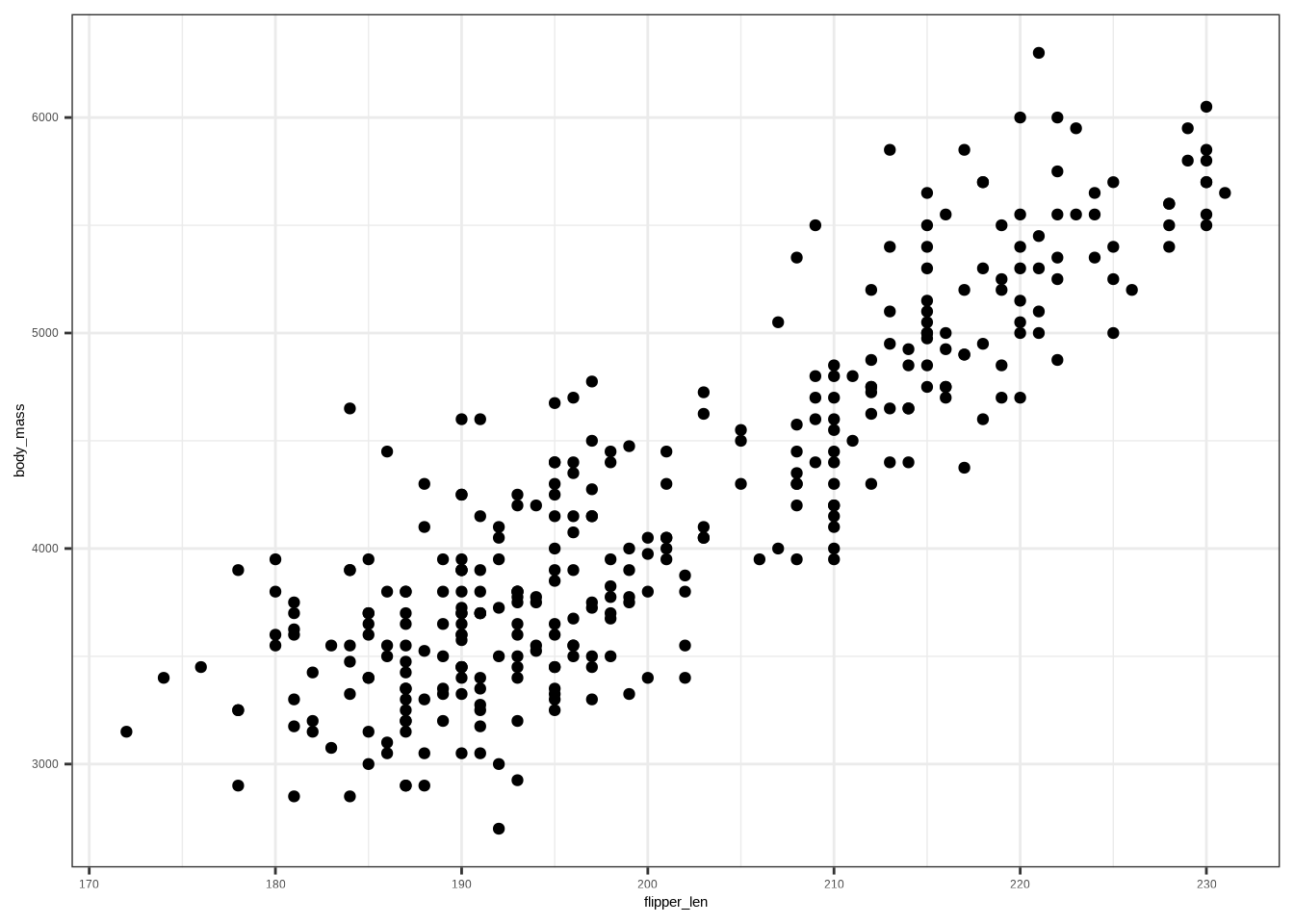
Copy the following code and put it in a code cell in Google Colab. Only do this if you are using a completely new notebook.

# This code will load the R packages we will use
install.packages(c("rcistats", "taylor",,
                 repos = c("https://inqs909.r-universe.dev", 
                           "https://cloud.r-project.org"))

# Uncomment and run for themes
# csucistats::install_themes()
# library(ThemePark)
# library(ggthemes)

library(rcistats)
library(tidyverse)
library(taylor)

1.2 Using the templates: what to change

DATA → your data frame/tibble (e.g., penguins)
Y → the outcome variable (e.g., body_mass_g)
X, X1, X2, …, Xp → predictor variables (e.g flipper_length_mm, species)
For categorical predictors: ensure the predictor is a factor (use factor(X) if needed).

2 Visualizing Variables

2.1 Scatter Plot (Continuous vs Continuous)

A scatter plot reveals association, trend direction, and form.

Template:

ggplot(DATA, aes(x = VAR1, y = VAR2)) +
  geom_point()

Example:

ggplot(penguins, aes(x = flipper_len, y = body_mass)) +
  geom_point()

2.2 Multi Densigy Plot (Continuous vs Categorical)

A density plot is a way to visualize the distribution of a continuous variable — it shows where data values are concentrated (dense) and where they are sparse.

Template:

ggplot(DATA, aes(x = NUM, color = CAT)) +
  geom_density()

Example:

ggplot(penguins, aes(x = flipper_len, color = species)) +
  geom_density()

Template:

ggplot(DATA, aes(x = NUM, fill = CAT)) +
  geom_density()

Example:

ggplot(penguins, aes(x = flipper_len, group = species)) +
  geom_density()

Template:

ggplot(DATA, aes(x = NUM, group = CAT)) +
  geom_density()

Example:

ggplot(penguins, aes(x = flipper_len, group = species)) +
  geom_density()

2.3 Multi Box Plot (Continuous vs Categorical)

A box plot summarizes median, quartiles, and potential outliers.

Template:

ggplot(DATA, aes(x = NUM, y = CAT)) +
  geom_boxplot()

Example:

ggplot(penguins, aes(x = flipper_len, y = species)) +
  geom_boxplot()

3 Modeling Relationships

3.1 Explaining variation

This is the process of trying to reduce unexplained variation in an outcome by using informative predictors — think getting it less wrong with an educated guess.

ggplot(penguins, aes(body_mass)) +
  geom_density()

If we know some information, we can get less wrong over time.

# Same variable, grouped by a category (species)
ggplot(penguins, aes(body_mass, fill = species)) +
  geom_density(alpha = .5)

3.2 A simple model (intercept-only)

We believe the outcome ($Y$) is generated by an unknown data generated process ($DGP_1$): $Y \sim DGP_1$. A minimal model says all outcomes are generated from a number (labeled as $\beta_0$) plus or minus some error ($\varepsilon$):
\[ Y = \beta_0 + \varepsilon \]

This is known as a simple model and the errors are simulated by a different DGP $\varepsilon \sim DGP_2$. The simple model is unknown, so we construct and estimated simple model for our best guess on how the data is generated:

\[ \hat Y = \hat\beta_0 \]

The carats above the letters are known as hats, which means best guess.

Tip

Observed vs. estimated:

Observed $Y = \beta_0 + \varepsilon$
Estimated $\hat Y = \hat\beta_0$

3.2.1 Fitting Simple Model

Template:

lm(Y ~ 1, data = DATA)

DATA → your data (e.g., penguins).
Y → the outcome variable (e.g., body_mass_g).

Example:

# Fit the null (intercept-only) model
m0 <- lm(body_mass ~ 1, data = penguins)
m0

#> 
#> Call:
#> lm(formula = body_mass ~ 1, data = penguins)
#> 
#> Coefficients:
#> (Intercept)  
#>        4207

3.3 Linear regression model with one predictor

Model form:

\[ Y = \beta_0 + \beta_1 X + \varepsilon, \quad \hat Y = \hat\beta_0 + \hat\beta_1 X. \]

# Scatter plot
ggplot(penguins, aes(flipper_len, body_mass)) +
  geom_point()

# Add a least-squares line
ggplot(penguins, aes(flipper_len, body_mass)) +
  geom_point() +
  stat_smooth(method = "lm", se = FALSE)

# Fit the model
m1 <- lm(body_mass ~ flipper_len, data = penguins)
m1

#> 
#> Call:
#> lm(formula = body_mass ~ flipper_len, data = penguins)
#> 
#> Coefficients:
#> (Intercept)  flipper_len  
#>    -5872.09        50.15

Template:

lm(Y ~ X, data = DATA)

4 Categorical predictors (dummy variables)

When we use a categorical predictor in a regression, R needs to convert the categories into numbers. This is done using dummy variables (also called indicator variables).

4.1 General idea

Suppose we have a categorical variable with C categories.
We create C − 1 dummy variables, each taking value:
- 1 if the observation belongs to that category
- 0 otherwise
The category without a dummy variable becomes the reference (baseline) group.

Example: Penguin species:

The species variable has 3 categories: Adelie, Chinstrap, Gentoo.

We create two dummy variables:

$D_1$: 1 if Chinstrap, 0 otherwise
$D_2$: 1 if Gentoo, 0 otherwise
Adelie is the reference (when both $D_1 = 0, D_2 = 0$)

Species	$D_1$ (Chinstrap)	$D_2$ (Gentoo)
Adelie	0	0
Chinstrap	1	0
Gentoo	0	1

4.2 Regression model with dummy variables

If we model penguin body mass ($Y$) with species:

\[ \hat Y_i = \beta_0 + \beta_1 D_{1i} + \beta_2 D_{2i} \]

$\beta_0$: mean of Adelie (reference group)
$\beta_1$: difference in mean body mass between Chinstrap and Adelie
$\beta_2$: difference in mean body mass between Gentoo and Adelie

Predictions:
- Adelie: $\hat Y = \beta_0$
- Chinstrap: $\hat Y = \beta_0 + \beta_1$
- Gentoo: $\hat Y = \beta_0 + \beta_2$

4.3 R Implementation

R automatically creates dummy variables when you use a factor in lm().
The first level of the factor is used as the reference group (by default).

# Fit model with species (factor) as predictor
m <- lm(body_mass ~ species, data = penguins)
summary(m)

#> 
#> Call:
#> lm(formula = body_mass ~ species, data = penguins)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -1142.44  -342.44   -33.09   307.56  1207.56 
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)       3706.16      38.14  97.184   <2e-16 ***
#> speciesChinstrap    26.92      67.65   0.398    0.691    
#> speciesGentoo     1386.27      56.91  24.359   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 460.8 on 330 degrees of freedom
#> Multiple R-squared:  0.6745, Adjusted R-squared:  0.6725 
#> F-statistic: 341.9 on 2 and 330 DF,  p-value: < 2.2e-16

Templates:

lm(Y ~ X, data = DATA)           # if X is already a factor
lm(Y ~ factor(X), data = DATA)   # force X to be treated as factor

4.4 Group Statistics

The function num_by_cat_stats() quickly computes descriptive statistics of a numerical variable grouped by a categorical variable.

Template:

num_by_cat_stats(DATA, NUM, CAT)

DATA: the data frame (e.g., penguins)
NUM: the numerical variable you want to summarize (e.g., body_mass_g)
CAT: the categorical variable that defines groups (e.g., species)

Example:

num_by_cat_stats(penguins, body_mass, species)

#>   Categories  min    q25     mean median  q75  max      sd      var   iqr
#> 1     Adelie 2850 3362.5 3706.164   3700 4000 4775 458.620 210332.4 637.5
#> 2  Chinstrap 2700 3487.5 3733.088   3700 3950 4800 384.335 147713.5 462.5
#> 3     Gentoo 3950 4700.0 5092.437   5050 5500 6300 501.476 251478.3 800.0
#>   missing
#> 1       0
#> 2       0
#> 3       0

5 Strength & correlation

Correlation (two numerical variables): $-1 \le r \le 1$. For simple linear regression, $R^2 = r^2$.

cor(penguins$body_mass, penguins$flipper_len)

#> [1] 0.8729789

# R^2 helper
r2(lm(body_mass ~ flipper_leng, data = penguins))

#> Error:
#> ! object 'flipper_leng' not found

Template:

# Correlation
cor(DATA$Y, DATA$X)

## R-Squared
xlm <- lm(Y ~ X, data = DATA); 
r2(xlm)

6 Prediction

Model: $\hat Y = \hat\beta_0 + \hat\beta_1 X$. Supply new X to get a prediction $\hat Y$.

Template:

m <- lm(Y ~ X, data = DATA)
ndf <- data.frame(X = VAL)
predict(m, newdata = ndf)

Examples:

xlm1 <- lm(body_mass ~ species, data = penguins)
predict(xlm1, newdata = data.frame(species = "Gentoo"))

#>        1 
#> 5092.437

xlm2 <- lm(body_mass ~ flipper_len, data = penguins)
predict(xlm2, newdata = data.frame(flipper_len = 190))

#>        1 
#> 3657.028

7 Multiple linear regression (MLR)

Model: $Y = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p + \varepsilon$

Template:

lm(Y ~ X1 + X2 + ... + Xp, data = DATA)

Example: danceability ~ mode_name + valence + energy

# Example: danceability ~ mode_name + valence + energy
lm(danceability ~ mode_name + valence + energy, data = taylor_album_songs)

#> 
#> Call:
#> lm(formula = danceability ~ mode_name + valence + energy, data = taylor_album_songs)
#> 
#> Coefficients:
#>    (Intercept)  mode_nameminor         valence          energy  
#>        0.53816         0.08386         0.17554        -0.05944

7.1 Adjusted $R^2$

\[R^2 = 1 - \frac{\text{Var(resid)}}{\text{Var}(Y)}, \quad R^2_{adj} = 1 - \Big(\frac{\text{Var(resid)}}{\text{Var}(Y)}\Big) \cdot \frac{n-1}{n-k-1}\]

m <- lm(danceability ~ mode_name + valence + energy, data = taylor_album_songs)
ar2(m)

#> [1] 0.09148268

8 Appendix: quick templates (copy‑paste)

8.1 Simple Model

lm(Y ~ 1, data = DATA)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)

8.2 Simple linear regression

lm(Y ~ X, data = DATA)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g flipper_length_mm)

8.3 SLR: Categorical predictor

lm(Y ~ X, data = DATA)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g species)

8.4 SLR: Categorical predictor (Create Factor)

lm(Y ~ factor(X), data = DATA)   # coerce X to factor

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g species)

8.5 Numerical Statistics by Categories

num_by_cat_stats(DATA, NUM, CAT)

DATA: the data frame (e.g., penguins)
NUM: the numerical variable you want to summarize (e.g., body_mass)
CAT: the categorical variable that defines groups (e.g., species)

8.6 Correlation

cor(DATA$Y, DATA$X, use = "complete.obs")

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g flipper_len)

8.7 $R^2$

m <- lm(Y ~ X, data = DATA)
r2(m)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g flipper_len)

8.8 Multiple linear regression

lm(Y ~ X1 + X2 + ... + Xp, data = DATA)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X1, X2, …, Xp → predictor variables (e.g flipper_len, species)

8.9 Adjusted $R^2$

# Adjusted R^2
m <- lm(Y ~ X1 + X2 + ... + Xp, data = DATA)
ar2(m)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X1, X2, …, Xp → predictor variables (e.g flipper_len, species)

8.10 Prediction: SLR

m <- lm(Y ~ X, data = DATA)
ndf <- data.frame(X = VAL)
predict(m, newdata = ndf)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X → predictor variables (e.g flipper_len)

8.11 Prediction: MLR

m <- lm(Y ~ X1 + X2 + ... + Xp, data = DATA)
ndf <- data.frame(X1 = VAL1, X2 = VAL2, ..., Xp = VALp)
predict(m, newdata = ndf)

DATA → your data frame (e.g., penguins)
Y → the outcome variable (e.g., body_mass)
X1, X2, …, Xp → predictor variables (e.g flipper_len, species)
VAL1, VAL2, …, VALp → predictor values (e.g 150, "Gentoo")

8.12 Scatter Plot

ggplot(DATA, aes(x = VAR1, y = VAR2)) + 
    geom_point()

DATA → the name of your dataset (e.g., penguins).
VAR1 → a single numerical variable (e.g., body_mass).
VAR2 → a single numerical variable (e.g., flipper_len).

8.13 Scatter Plot + trend line

ggplot(DATA, aes(x = VAR1, y = VAR2)) + 
    geom_point() + 
    geom_smooth(method = "lm", se = TRUE)

DATA → the name of your dataset (e.g., penguins).
VAR1 → a single numerical variable (e.g., body_mass).
VAR2 → a single numerical variable (e.g., flipper_len).

8.14 Multiple Density Plot (Continous vs Categorical)

ggplot(DATA, aes(x = NUM, color = CAT)) + 
    geom_density()

DATA → the name of your dataset (e.g., penguins).
NUM → a single numerical variable (e.g., body_mass).
CAT → a single categorical variable (e.g., species).

8.15 Multiple Box Plots (Continous vs Categorical)

ggplot(DATA, aes(x = NUM, y = CAT)) + 
    geom_boxplot()

DATA → the name of your dataset (e.g., penguins).
NUM → a single numerical variable (e.g., body_mass).
CAT → a single categorical variable (e.g., species).

--- title: "Linear Regression Models" description: "Explaining variation, simple & multiple linear models, categorical predictors, correlation, and prediction" format: html: toc: true toc-depth: 3 number-sections: true code-tools: true code-fold: false smooth-scroll: true editor: source image: img/linear.png execute: echo: true warning: false message: false error: true jupyter: r knitr: opts_chunk: comment: "#>" --- # Setup ```{r} #| label: setup #| include: false library(tidyverse) library(rcistats) library(ThemePark) library(taylor) library(DT) penguins <- penguins |> drop_na() theme_set(theme_bw()) ``` ## Google Colab Copy the following code and put it in a code cell in Google Colab. Only do this if you are using a completely new notebook. ``` r # This code will load the R packages we will use install.packages(c("rcistats", "taylor",, repos = c("https://inqs909.r-universe.dev", "https://cloud.r-project.org")) # Uncomment and run for themes # csucistats::install_themes() # library(ThemePark) # library(ggthemes) library(rcistats) library(tidyverse) library(taylor) ``` ## Using the templates: what to change - **`DATA`** → your data frame/tibble (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass_g`) - **`X`, `X1`, `X2`, ..., `Xp`** → predictor variables (e.g `flipper_length_mm`, `species`) - For categorical predictors: ensure the predictor is a **factor** (use `factor(X)` if needed). # Visualizing Variables ## Scatter Plot (Continuous vs Continuous) A **scatter plot** reveals association, trend direction, and form. **Template:** ```r ggplot(DATA, aes(x = VAR1, y = VAR2)) + geom_point() ``` **Example:** ```{r} ggplot(penguins, aes(x = flipper_len, y = body_mass)) + geom_point() ``` ## Multi Densigy Plot (Continuous vs Categorical) A density plot is a way to visualize the distribution of a continuous variable — it shows where data values are concentrated (dense) and where they are sparse. ::: panel-tabset ### Color **Template:** ```r ggplot(DATA, aes(x = NUM, color = CAT)) + geom_density() ``` **Example:** ```{r} ggplot(penguins, aes(x = flipper_len, color = species)) + geom_density() ``` ### Fill **Template:** ```r ggplot(DATA, aes(x = NUM, fill = CAT)) + geom_density() ``` **Example:** ```{r} ggplot(penguins, aes(x = flipper_len, group = species)) + geom_density() ``` ### Group **Template:** ```r ggplot(DATA, aes(x = NUM, group = CAT)) + geom_density() ``` **Example:** ```{r} ggplot(penguins, aes(x = flipper_len, group = species)) + geom_density() ``` ::: ## Multi Box Plot (Continuous vs Categorical) A **box plot** summarizes median, quartiles, and potential outliers. **Template:** ```r ggplot(DATA, aes(x = NUM, y = CAT)) + geom_boxplot() ``` **Example:** ```{r} ggplot(penguins, aes(x = flipper_len, y = species)) + geom_boxplot() ``` # Modeling Relationships ## Explaining variation This is the process of trying to **reduce unexplained variation** in an outcome by using informative predictors — think *getting it less wrong* with an educated guess. ```{r} #| label: fig-plot-1 ggplot(penguins, aes(body_mass)) + geom_density() ``` If we know some information, we can get less wrong over time. ```{r} # Same variable, grouped by a category (species) ggplot(penguins, aes(body_mass, fill = species)) + geom_density(alpha = .5) ``` ## A simple model (intercept-only) We believe the outcome ($Y$) is generated by an unknown data generated process ($DGP_1$): $Y \sim DGP_1$. A minimal model says all outcomes are generated from a number (labeled as $\beta_0$) plus or minus some error ($\varepsilon$):\ $$ Y = \beta_0 + \varepsilon $$ This is known as a simple model and the errors are simulated by a different DGP $\varepsilon \sim DGP_2$. The simple model is unknown, so we construct and estimated simple model for our best guess on how the data is generated: $$ \hat Y = \hat\beta_0 $$ The carats above the letters are known as hats, which means best guess. ::: callout-tip **Observed vs. estimated:** - Observed $Y = \beta_0 + \varepsilon$ - Estimated $\hat Y = \hat\beta_0$ ::: ### Fitting Simple Model **Template:** ``` r lm(Y ~ 1, data = DATA) ``` - **`DATA`** → your data (e.g., `penguins`).\ - **`Y`** → the outcome variable (e.g., `body_mass_g`). 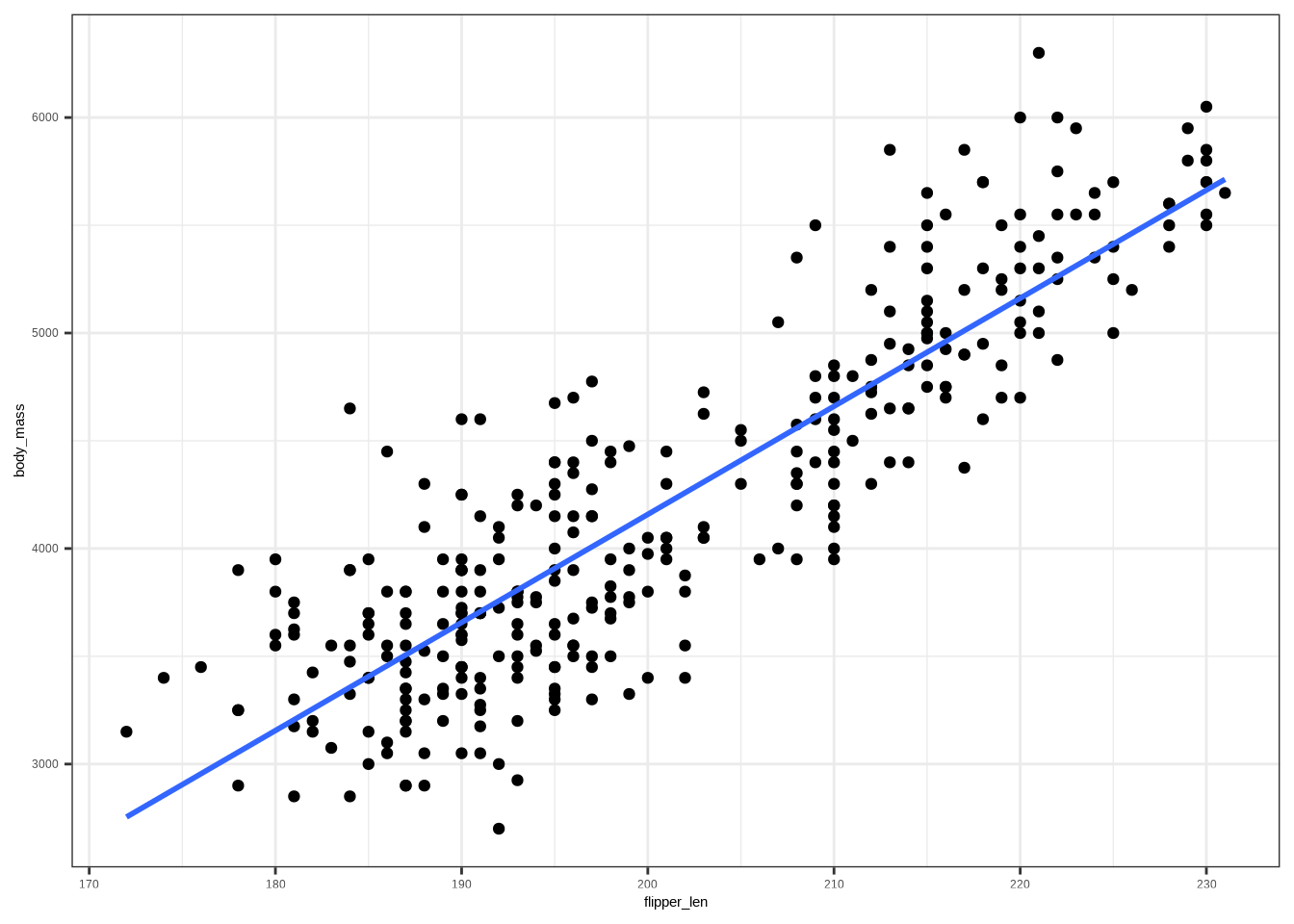**Example:** ```{r} # Fit the null (intercept-only) model m0 <- lm(body_mass ~ 1, data = penguins) m0 ``` ## Linear regression model with one predictor **Model form:** $$ Y = \beta_0 + \beta_1 X + \varepsilon, \quad \hat Y = \hat\beta_0 + \hat\beta_1 X. $$ ```{r} # Scatter plot ggplot(penguins, aes(flipper_len, body_mass)) + geom_point() ``` ```{r} # Add a least-squares line ggplot(penguins, aes(flipper_len, body_mass)) + geom_point() + stat_smooth(method = "lm", se = FALSE) ``` ```{r} # Fit the model m1 <- lm(body_mass ~ flipper_len, data = penguins) m1 ``` **Template:** ``` r lm(Y ~ X, data = DATA) ``` # Categorical predictors (dummy variables) When we use a **categorical predictor** in a regression, R needs to convert the categories into numbers. This is done using **dummy variables** (also called indicator variables). ## General idea - Suppose we have a categorical variable with **C categories**.\ - We create **C − 1 dummy variables**, each taking value: - `1` if the observation belongs to that category\ - `0` otherwise\ - The category without a dummy variable becomes the **reference (baseline)** group. **Example: Penguin species:** The `species` variable has 3 categories: **Adelie, Chinstrap, Gentoo**. We create two dummy variables: - $D_1$: 1 if Chinstrap, 0 otherwise\ - $D_2$: 1 if Gentoo, 0 otherwise\ - Adelie is the reference (when both $D_1 = 0, D_2 = 0$) | Species | $D_1$ (Chinstrap) | $D_2$ (Gentoo) | |-----------|-------------------|----------------| | Adelie | 0 | 0 | | Chinstrap | 1 | 0 | | Gentoo | 0 | 1 | ## Regression model with dummy variables If we model penguin body mass ($Y$) with species: $$ \hat Y_i = \beta_0 + \beta_1 D_{1i} + \beta_2 D_{2i} $$ - $\beta_0$: mean of Adelie (reference group)\ - $\beta_1$: difference in mean body mass between Chinstrap and Adelie\ - $\beta_2$: difference in mean body mass between Gentoo and Adelie Predictions:\ - Adelie: $\hat Y = \beta_0$\ - Chinstrap: $\hat Y = \beta_0 + \beta_1$\ - Gentoo: $\hat Y = \beta_0 + \beta_2$ ## R Implementation R automatically creates dummy variables when you use a factor in `lm()`.\ The first level of the factor is used as the **reference group** (by default). ```{r} # Fit model with species (factor) as predictor m <- lm(body_mass ~ species, data = penguins) summary(m) ``` **Templates:** ``` r lm(Y ~ X, data = DATA) # if X is already a factor lm(Y ~ factor(X), data = DATA) # force X to be treated as factor ``` ## Group Statistics The function `num_by_cat_stats()` quickly computes **descriptive statistics of a numerical variable grouped by a categorical variable**. **Template:** ``` r num_by_cat_stats(DATA, NUM, CAT) ``` - `DATA`: the data frame (e.g., `penguins`) - `NUM`: the numerical variable you want to summarize (e.g., `body_mass_g`) - `CAT`: the categorical variable that defines groups (e.g., `species`) **Example:** ```{r} num_by_cat_stats(penguins, body_mass, species) ``` # Strength & correlation Correlation (two numerical variables): $-1 \le r \le 1$. For simple linear regression, $R^2 = r^2$. ```{r} cor(penguins$body_mass, penguins$flipper_len) ``` ```{r} # R^2 helper r2(lm(body_mass ~ flipper_leng, data = penguins)) ``` **Template:** ``` r # Correlation cor(DATA$Y, DATA$X) ## R-Squared xlm <- lm(Y ~ X, data = DATA); r2(xlm) ``` # Prediction Model: $\hat Y = \hat\beta_0 + \hat\beta_1 X$. Supply new X to get a prediction $\hat Y$. **Template:** ``` r m <- lm(Y ~ X, data = DATA) ndf <- data.frame(X = VAL) predict(m, newdata = ndf) ``` **Examples:** ```{r} xlm1 <- lm(body_mass ~ species, data = penguins) predict(xlm1, newdata = data.frame(species = "Gentoo")) ``` ```{r} xlm2 <- lm(body_mass ~ flipper_len, data = penguins) predict(xlm2, newdata = data.frame(flipper_len = 190)) ``` # Multiple linear regression (MLR) Model: $Y = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p + \varepsilon$ **Template:** ``` r lm(Y ~ X1 + X2 + ... + Xp, data = DATA) ``` **Example: danceability \~ mode_name + valence + energy** ```{r} # Example: danceability ~ mode_name + valence + energy lm(danceability ~ mode_name + valence + energy, data = taylor_album_songs) ``` ## Adjusted $R^2$ $$R^2 = 1 - \frac{\text{Var(resid)}}{\text{Var}(Y)}, \quad R^2_{adj} = 1 - \Big(\frac{\text{Var(resid)}}{\text{Var}(Y)}\Big) \cdot \frac{n-1}{n-k-1}$$ ```{r} m <- lm(danceability ~ mode_name + valence + energy, data = taylor_album_songs) ar2(m) ``` # Appendix: quick templates (copy‑paste) ## Simple Model ``` r lm(Y ~ 1, data = DATA) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) ## Simple linear regression ``` r lm(Y ~ X, data = DATA) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `flipper_length_mm`) ## SLR: Categorical predictor ``` r lm(Y ~ X, data = DATA) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `species`) ## SLR: Categorical predictor (Create Factor) ``` r lm(Y ~ factor(X), data = DATA) # coerce X to factor ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `species`) ## Numerical Statistics by Categories ``` r num_by_cat_stats(DATA, NUM, CAT) ``` - `DATA`: the data frame (e.g., `penguins`) - `NUM`: the numerical variable you want to summarize (e.g., `body_mass`) - `CAT`: the categorical variable that defines groups (e.g., `species`) ## Correlation ``` r cor(DATA$Y, DATA$X, use = "complete.obs") ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `flipper_len`) ## $R^2$ ``` r m <- lm(Y ~ X, data = DATA) r2(m) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `flipper_len`) ## Multiple linear regression ``` r lm(Y ~ X1 + X2 + ... + Xp, data = DATA) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `flipper_len`, `species`) ## Adjusted $R^2$ ``` r # Adjusted R^2 m <- lm(Y ~ X1 + X2 + ... + Xp, data = DATA) ar2(m) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `flipper_len`, `species`) ## Prediction: SLR ``` r m <- lm(Y ~ X, data = DATA) ndf <- data.frame(X = VAL) predict(m, newdata = ndf) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X`** → predictor variables (e.g `flipper_len`) ## Prediction: MLR ``` r m <- lm(Y ~ X1 + X2 + ... + Xp, data = DATA) ndf <- data.frame(X1 = VAL1, X2 = VAL2, ..., Xp = VALp) predict(m, newdata = ndf) ``` - **`DATA`** → your data frame (e.g., `penguins`) - **`Y`** → the outcome variable (e.g., `body_mass`) - **`X1`, `X2`, ..., `Xp`** → predictor variables (e.g `flipper_len`, `species`) - **`VAL1`, `VAL2`, ..., `VALp`** → predictor values (e.g `150`, `"Gentoo"`) ## Scatter Plot ```r ggplot(DATA, aes(x = VAR1, y = VAR2)) + geom_point() ``` - `DATA` → the name of your dataset (e.g., `penguins`). - `VAR1` → a single numerical variable (e.g., `body_mass`). - `VAR2` → a single numerical variable (e.g., `flipper_len`). ## Scatter Plot + trend line ```r ggplot(DATA, aes(x = VAR1, y = VAR2)) + geom_point() + geom_smooth(method = "lm", se = TRUE) ``` - `DATA` → the name of your dataset (e.g., `penguins`). - `VAR1` → a single numerical variable (e.g., `body_mass`). - `VAR2` → a single numerical variable (e.g., `flipper_len`). ## Multiple Density Plot (Continous vs Categorical) ```r ggplot(DATA, aes(x = NUM, color = CAT)) + geom_density() ``` - `DATA` → the name of your dataset (e.g., `penguins`). - `NUM` → a single numerical variable (e.g., `body_mass`). - `CAT` → a single categorical variable (e.g., `species`). ## Multiple Box Plots (Continous vs Categorical) ```r ggplot(DATA, aes(x = NUM, y = CAT)) + geom_boxplot() ``` - `DATA` → the name of your dataset (e.g., `penguins`). - `NUM` → a single numerical variable (e.g., `body_mass`). - `CAT` → a single categorical variable (e.g., `species`).

Linear Regression Models

1 Setup

1.1 Google Colab

1.2 Using the templates: what to change

2 Visualizing Variables

2.1 Scatter Plot (Continuous vs Continuous)

2.2 Multi Densigy Plot (Continuous vs Categorical)

2.3 Multi Box Plot (Continuous vs Categorical)

3 Modeling Relationships

3.1 Explaining variation

3.2 A simple model (intercept-only)

3.2.1 Fitting Simple Model

3.3 Linear regression model with one predictor

4 Categorical predictors (dummy variables)

4.1 General idea

4.2 Regression model with dummy variables

4.3 R Implementation

4.4 Group Statistics

5 Strength & correlation

6 Prediction

7 Multiple linear regression (MLR)

7.1 Adjusted \(R^2\)

8 Appendix: quick templates (copy‑paste)

8.1 Simple Model

8.2 Simple linear regression

8.3 SLR: Categorical predictor

8.4 SLR: Categorical predictor (Create Factor)

8.5 Numerical Statistics by Categories

8.6 Correlation

8.7 \(R^2\)

8.8 Multiple linear regression

8.9 Adjusted \(R^2\)

8.10 Prediction: SLR

8.11 Prediction: MLR

8.12 Scatter Plot

8.13 Scatter Plot + trend line

8.14 Multiple Density Plot (Continous vs Categorical)

8.15 Multiple Box Plots (Continous vs Categorical)