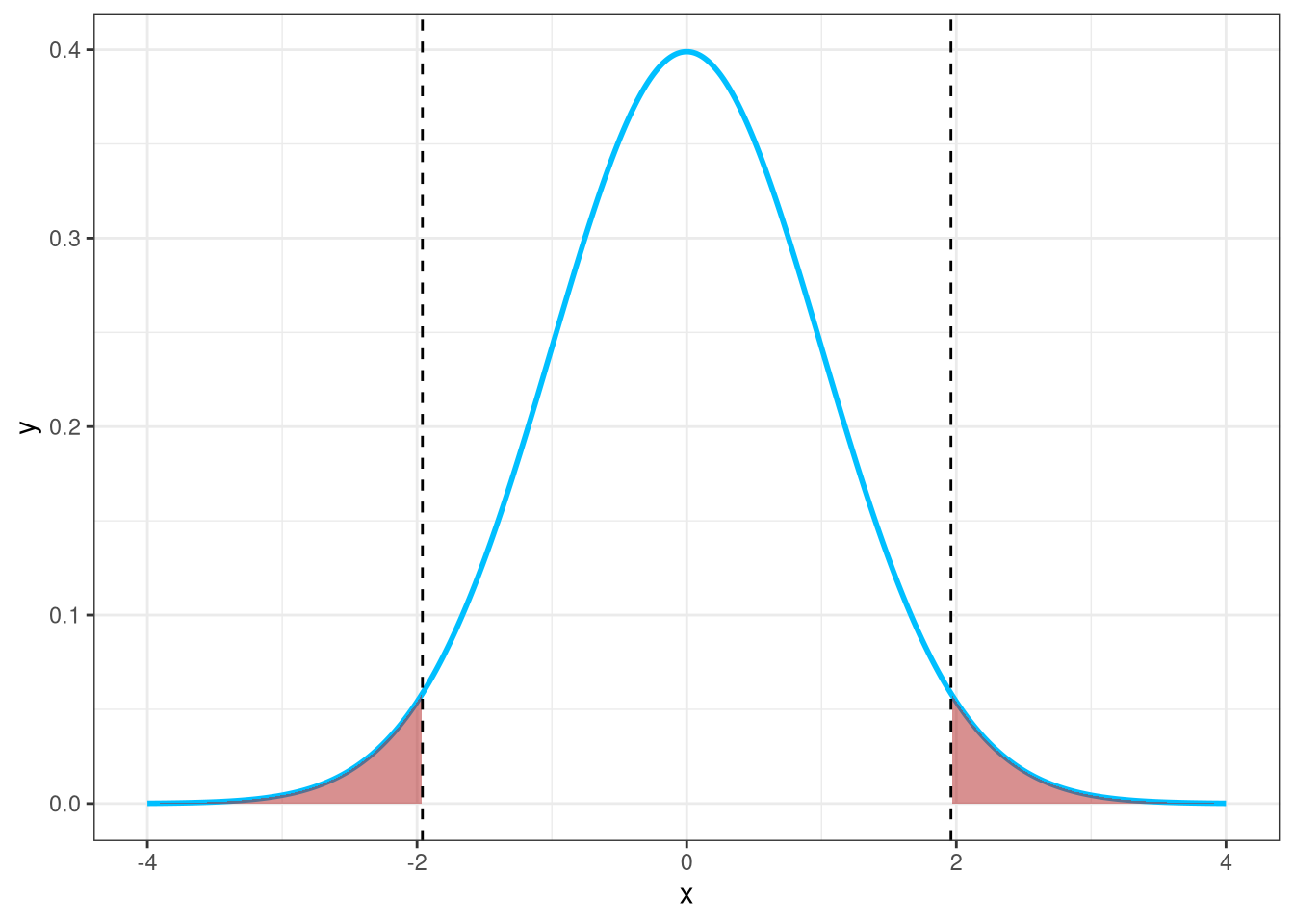
Code
alpha <- 0.05
# Critical values for two-tailed test
z_critical <- qnorm(1 - alpha / 2)
# Create data for the normal curve
x <- seq(-4, 4, length = 1000)
y <- dnorm(x)
df <- data.frame(x = x, y = y)
ggplot(df, aes(x = x, y = y)) +
geom_line(color = "deepskyblue", linewidth = 1) +
geom_area(data = subset(df, x <= -z_critical), aes(y = y), fill = "firebrick", alpha = 0.5) +
geom_area(data = subset(df, x >= z_critical), aes(y = y), fill = "firebrick", alpha = 0.5) +
geom_vline(xintercept = c(-z_critical, z_critical), linetype = "dashed", color = "black") +
theme_bw()