Sampling Distribution

Sampling Distribution

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Sampling Distribution

Sampling Distribution is the idea that the statistics that you generate (slopes and intercepts) have their own data generation process.

In other words, the numerical values you obtain from the lm and glm function can be different if we got a different data set.

Some values will be more common than others. Because of this, they have their own data generating process, like the outcome of interest has it’s own data generating process.

Sampling Distributions

  • Distribution of a statistic over repeated samples

  • Different Samples yield different statistics

Standard Error

The Standard Error (SE) is the standard deviation of a statistic itself.

SE tells us how much a statistic varies from sample to sample. Smaller SE = more precision.

Modelling the Data

\[ Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i \]

  • \(Y_i\): Outcome data
  • \(X_i\): Predictor data
  • \(\beta_0, \beta_1\): parameters
  • \(\varepsilon_i\): error term

Error Term

\[ \varepsilon_i \sim DGP \]

Randomness Effect

The randomness effect is a sampling phenomenom where you will get different samples every time you sample a population.

Getting different samples means you will get different statistics.

These statistics will have a distribution on their own.

Randomness Effect 1

Code 
x <- rnorm(1000)
y <- 4 + 5 * x + rnorm(1000)
bb <- round(b(lm(y ~ x),1),2)
ggplot(tibble(x = x, y = y), aes(x,y)) +
  geom_point() +
  annotate("text", 
           x = -1, y = 15, 
           label = TeX(sprintf(r'($\hat{\beta} = %g$)', bb),
                       output = "character"),
           parse = TRUE,
           size = 8)

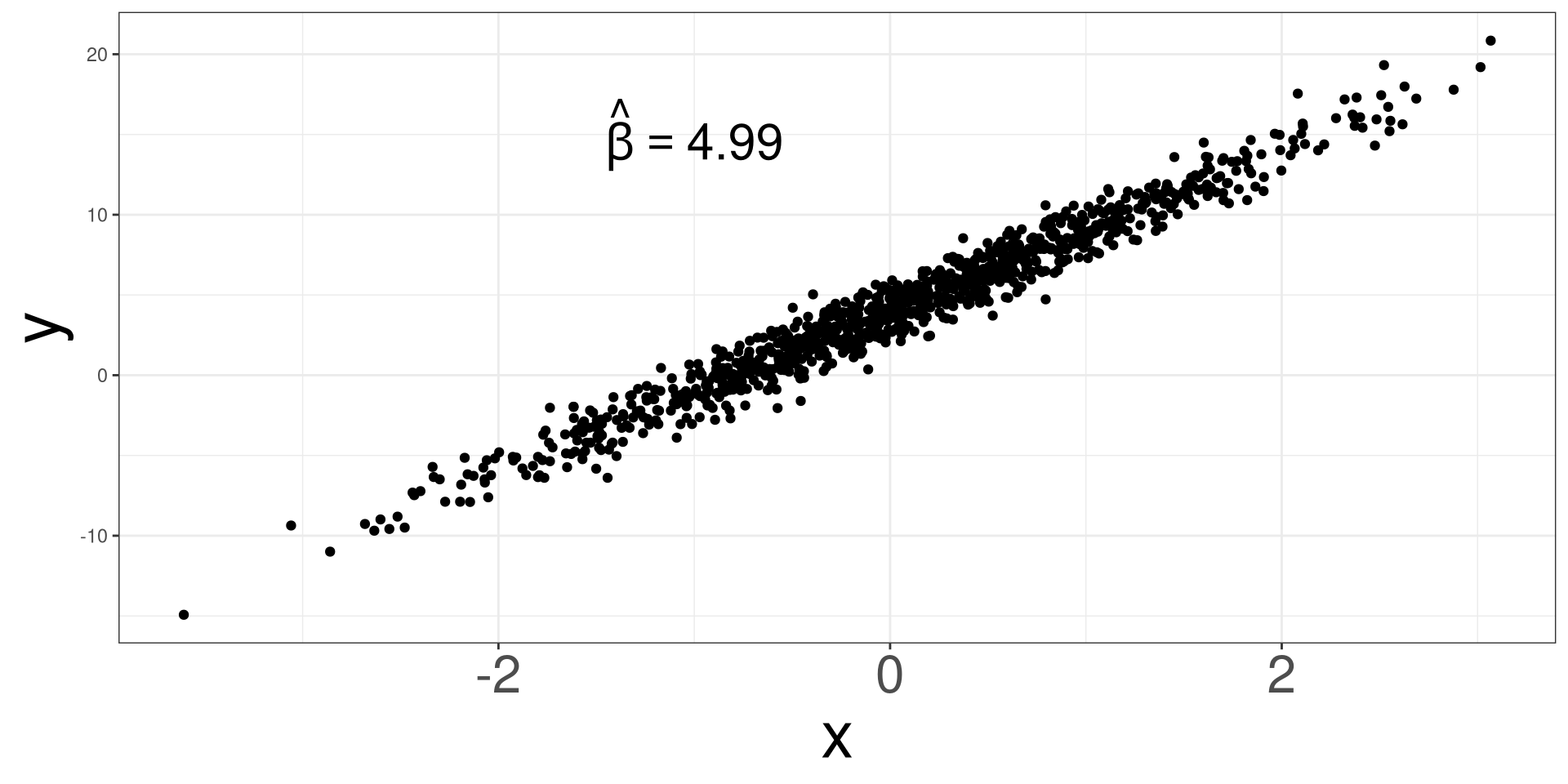
Randomness Effect 2

Code 
x <- rnorm(1000)
y <- 4 + 5 * x + rnorm(1000)
bb <- round(b(lm(y ~ x),1),2)
ggplot(tibble(x = x, y = y), aes(x,y)) +
  geom_point() +
  annotate("text", 
           x = -1, y = 15, 
           label = TeX(sprintf(r'($\hat{\beta} = %g$)', bb),
                       output = "character"),
           parse = TRUE,
           size = 8)

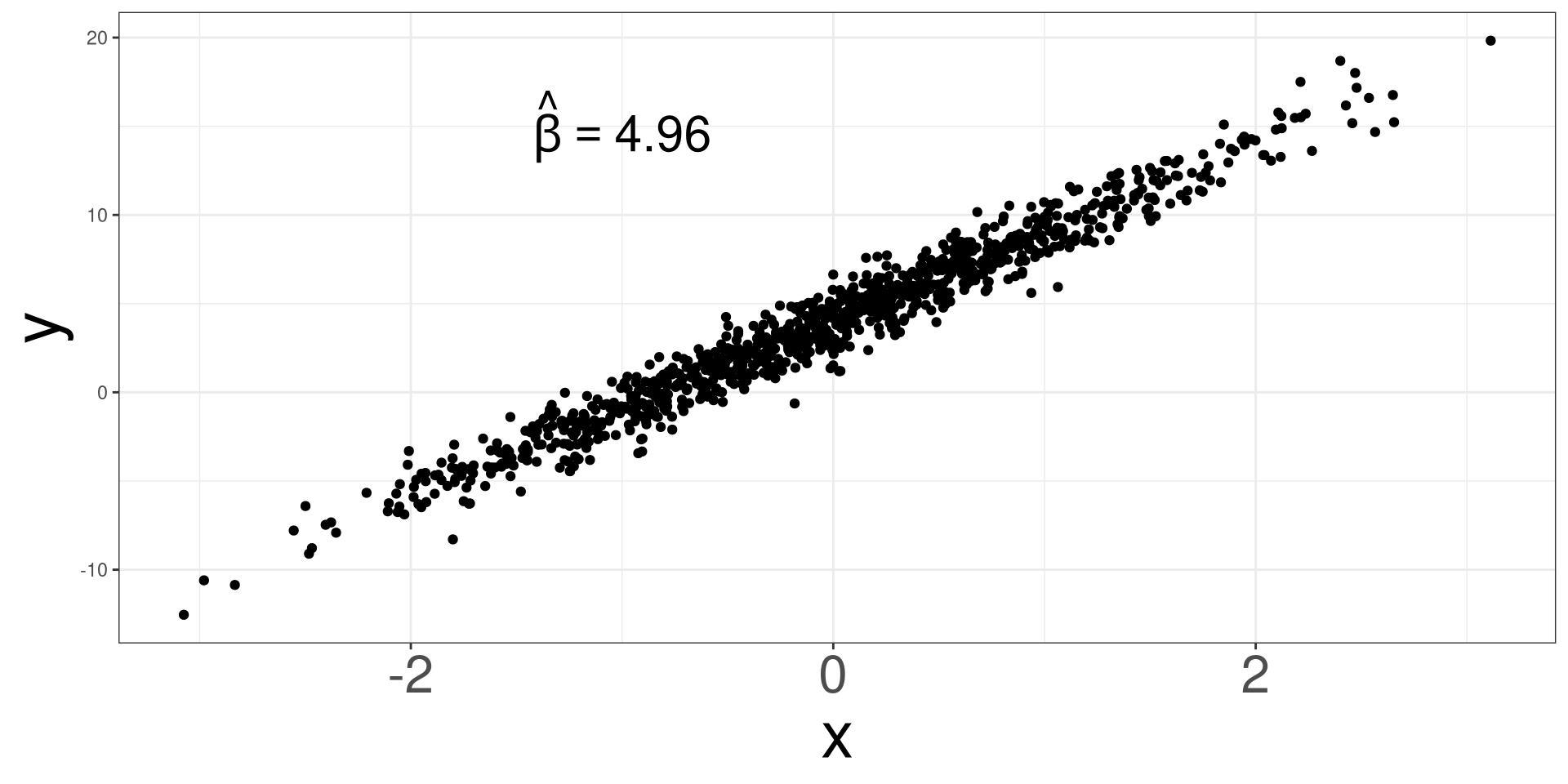
Randomness Effect 3

Code 
x <- rnorm(1000)
y <- 4 + 5 * x + rnorm(1000)
bb <- round(b(lm(y ~ x),1),2)
ggplot(tibble(x = x, y = y), aes(x,y)) +
  geom_point() +
  annotate("text", 
           x = -1, y = 15, 
           label = TeX(sprintf(r'($\hat{\beta} = %g$)', bb),
                       output = "character"),
           parse = TRUE,
           size = 8)

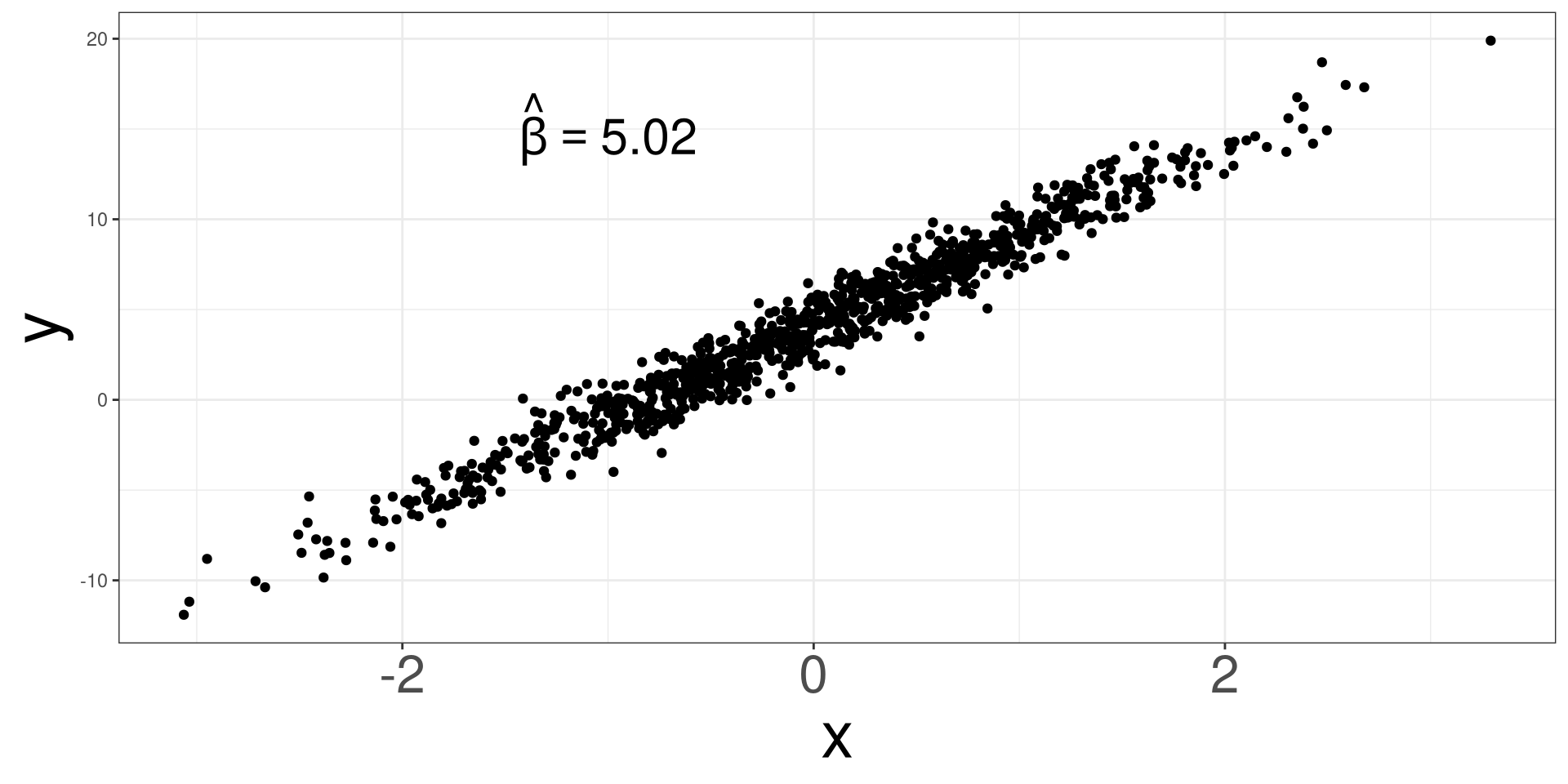
Randomness Effect 4

Code 
x <- rnorm(1000)
y <- 4 + 5 * x + rnorm(1000)
bb <- round(b(lm(y ~ x),1),2)
ggplot(tibble(x = x, y = y), aes(x,y)) +
  geom_point() +
  annotate("text", 
           x = -1, y = 15, 
           label = TeX(sprintf(r'($\hat{\beta} = %g$)', bb),
                       output = "character"),
           parse = TRUE,
           size = 8)

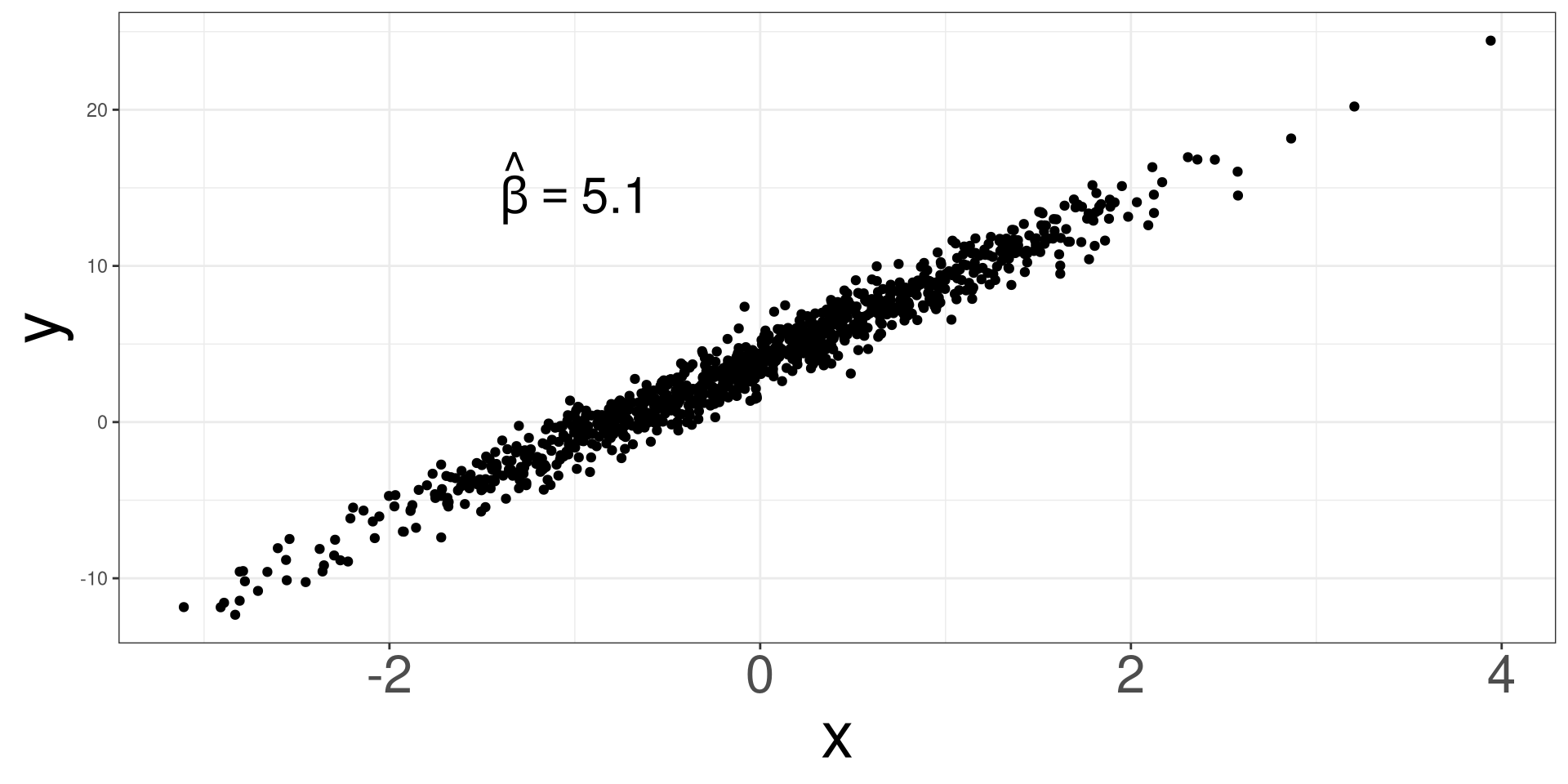
Randomness Effect 5

Code 
x <- rnorm(1000)
y <- 4 + 5 * x + rnorm(1000)
bb <- round(b(lm(y ~ x),1),2)
ggplot(tibble(x = x, y = y), aes(x,y)) +
  geom_point() +
  annotate("text", 
           x = -1, y = 15, 
           label = TeX(sprintf(r'($\hat{\beta} = %g$)', bb),
                       output = "character"),
           parse = TRUE,
           size = 8)

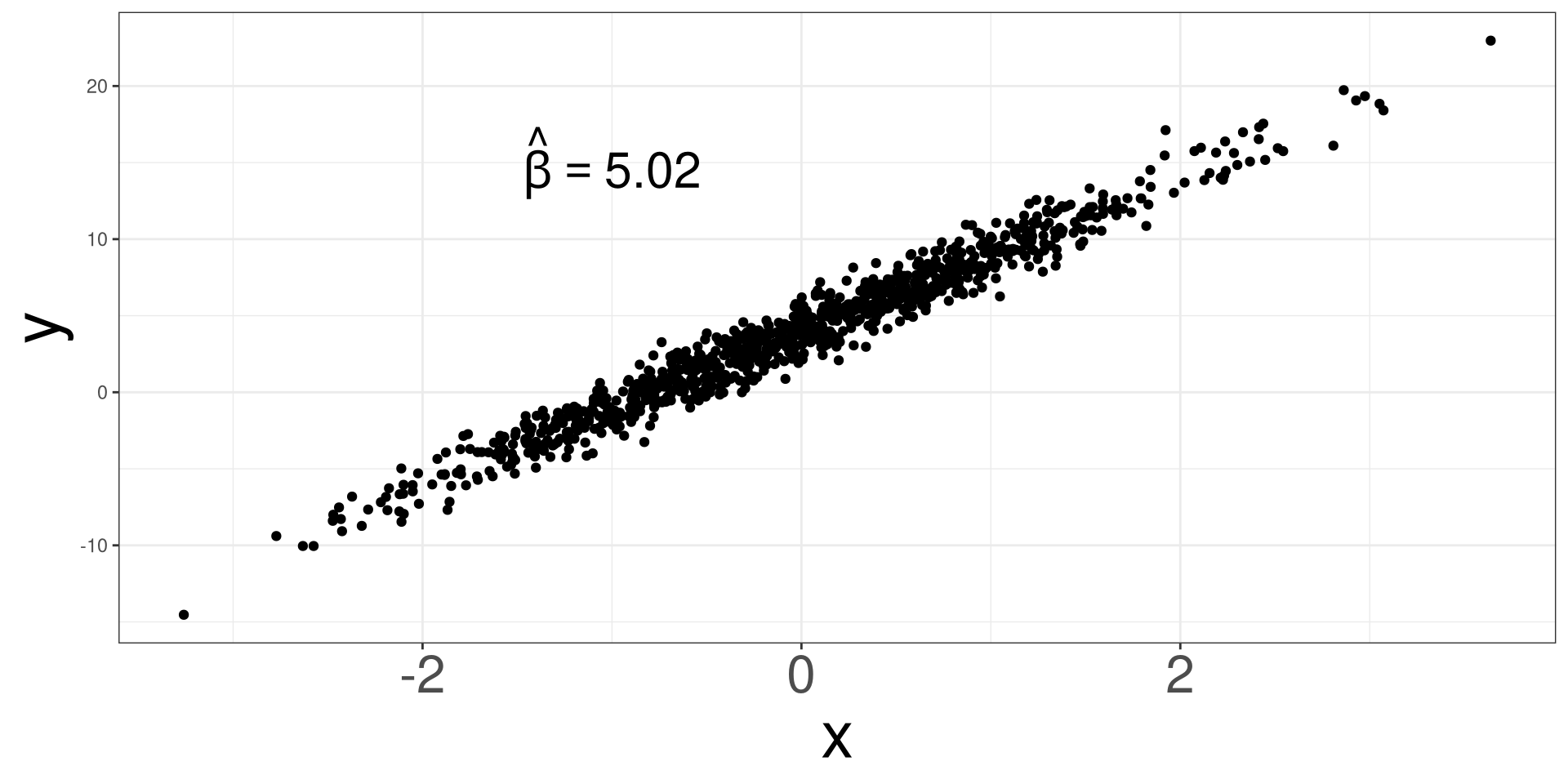
Simulating Unicorns

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Simulating Unicorns

To better understand the variation in statistics, let’s simulate a data set of unicorn characteristics to visualize and understand the variation.

We will simulate a data set using the unicorns function and only we need to specify how many unicorns you want to simulate.

Simulating Unicorn Data

Code 
unicorns(10)
#>    Unicorn_ID Age      Gender Color Type_of_Unicorn Type_of_Horn Horn_Length
#> 1           1  10  Non-binary  Gray           Ember         Opal    5.287256
#> 2           2  11 Genderfluid  Gray           Ember   Aquamarine    4.591308
#> 3           3   5      Female  Pink           Ember         Opal    4.992701
#> 4           4  14        Male White           Ember         Opal    4.352872
#> 5           5   4        Male Black           Ruvas         Opal    4.796048
#> 6           6   9  Non-binary White           Ember   Aquamarine    4.598019
#> 7           7  14        Male  Gray           Ruvas   Aquamarine    4.549760
#> 8           8  11     Agender Brown           Ember   Aquamarine    4.973695
#> 9           9  20     Agender  Gold           Jewel         Opal    4.864004
#> 10         10  10     Agender  Gold           Jewel         Opal    5.079095
#>    Horn_Strength   Weight Health_Score Personality_Score Magical_Score
#> 1       24.70889 137.6102            6       2.006764214      11015.19
#> 2       29.11632 134.6205            2       2.124926856      10995.41
#> 3       27.68589 108.5017            2       4.934695058      10853.76
#> 4       25.88500 142.4263            8       0.300370842      11115.87
#> 5       29.46725 126.5744            1       0.383786512      10817.42
#> 6       29.17967 127.9718            2       0.598821190      10941.86
#> 7       27.53249 129.6387            1       0.602664941      11084.51
#> 8       29.98466 123.6671           10       2.296081966      10999.39
#> 9       29.49899 137.9716            3       2.263051942      11301.22
#> 10      28.99222 138.5688            4       0.007638889      11029.60
#>    Elusiveness_Score Gentleness_Score Nature_Score
#> 1           40.51515        47.250604     948.9408
#> 2           36.25579        28.660853     946.0287
#> 3           35.91272         8.321457     929.1256
#> 4           36.80199        47.155697     961.3189
#> 5           36.16043        51.567881     924.2066
#> 6           37.81521         3.954338     939.3261
#> 7           35.94361        60.522925     957.9162
#> 8           33.01639        28.066502     946.7330
#> 9           38.16212        38.906987     984.1605
#> 10          37.94923       -35.147940     951.2351

Unicorn Data Variables

Code 
names(unicorns(10))
#>  [1] "Unicorn_ID"        "Age"               "Gender"           
#>  [4] "Color"             "Type_of_Unicorn"   "Type_of_Horn"     
#>  [7] "Horn_Length"       "Horn_Strength"     "Weight"           
#> [10] "Health_Score"      "Personality_Score" "Magical_Score"    
#> [13] "Elusiveness_Score" "Gentleness_Score"  "Nature_Score"

We will only look at Magical_Score and Nature_Score.

Magical and Nature Score

\[ Magical = 3423 + 8 \times Nature + \varepsilon \]

\[ \varepsilon \sim N(0, 3.24) \]

Simulating \(N(0, 3.24)\)

Code 
rnorm(1, 0, sqrt(3.24))
#> [1] -2.536894

Collecting

Code 
unicorns(10) |> select(Nature_Score, Magical_Score)
#>    Nature_Score Magical_Score
#> 1      935.8889      10905.84
#> 2      946.3246      10991.69
#> 3      948.3476      11010.05
#> 4      916.1127      10754.62
#> 5      921.3345      10795.69
#> 6      976.0663      11235.21
#> 7      925.0308      10821.14
#> 8      972.5116      11201.34
#> 9      918.7336      10774.94
#> 10     923.0343      10808.61

DGP of Magical Score 1

Code 
ggplot(unicorns(500), aes(Magical_Score)) +
  geom_density()

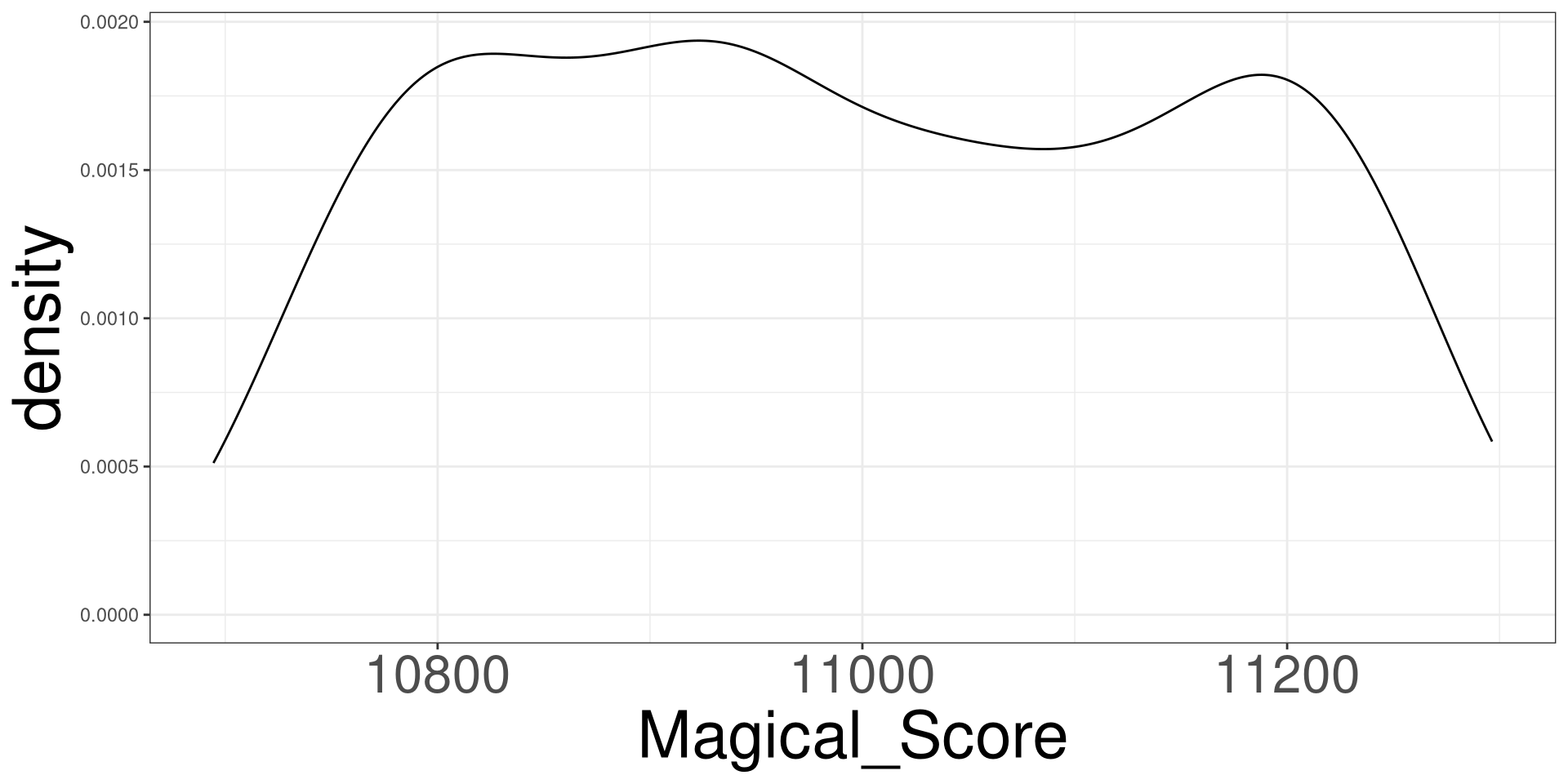
DGP of Magical Score 2

Code 
ggplot(unicorns(500), aes(Magical_Score)) +
  geom_density()

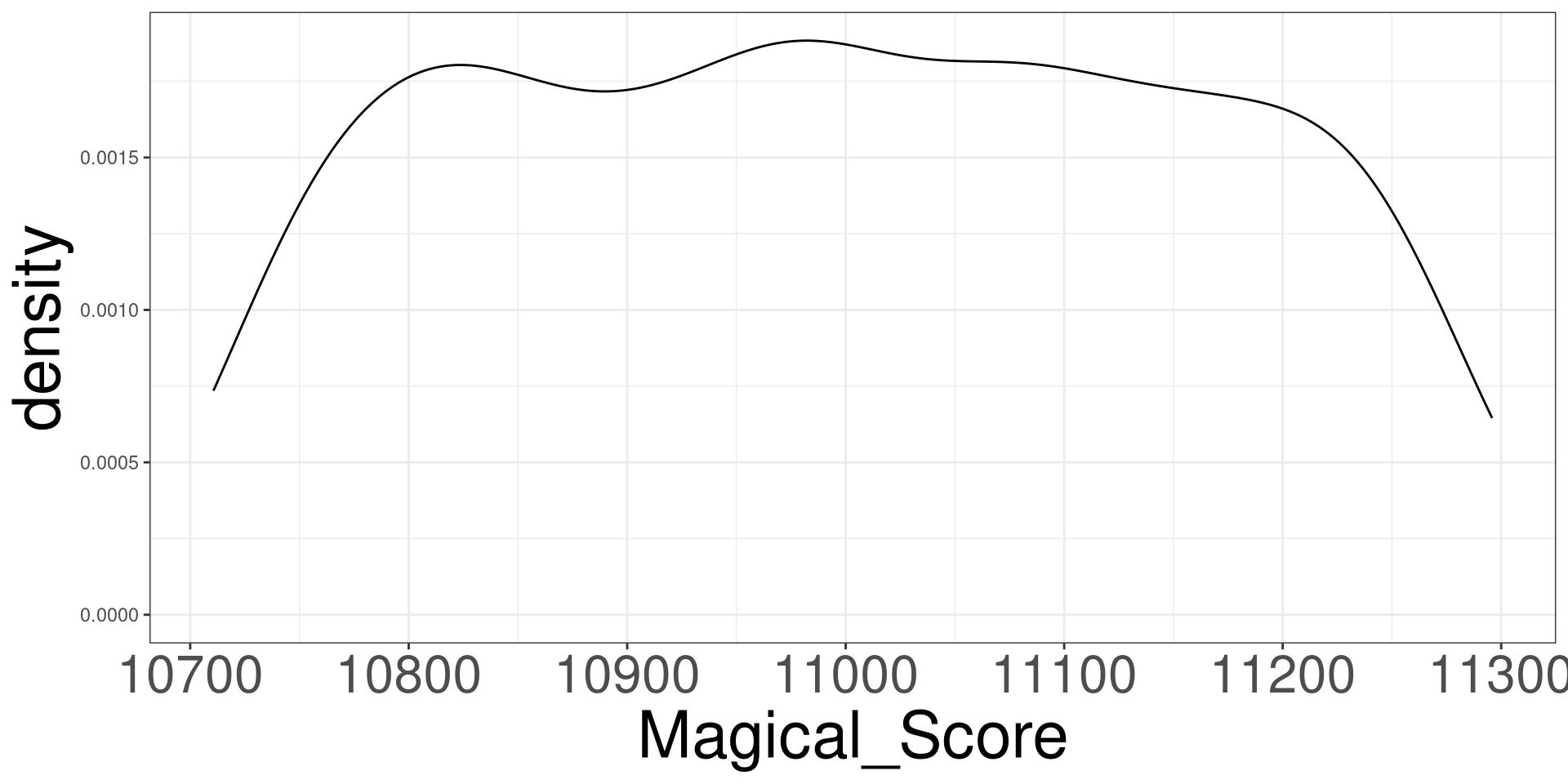
Estimating \(\beta_1\) via lm

Code 
u1 <- unicorns(500)
lm(Magical_Score ~ Nature_Score, u1)
#> 
#> Call:
#> lm(formula = Magical_Score ~ Nature_Score, data = u1)
#> 
#> Coefficients:
#>  (Intercept)  Nature_Score  
#>     3425.787         7.997

Collecting a new sample

Code 
u2 <- unicorns(500)
lm(Magical_Score ~ Nature_Score, u2)
#> 
#> Call:
#> lm(formula = Magical_Score ~ Nature_Score, data = u2)
#> 
#> Coefficients:
#>  (Intercept)  Nature_Score  
#>     3426.461         7.996

Collecting a new sample

Code 
u3 <- unicorns(500)
lm(Magical_Score ~ Nature_Score, u3)
#> 
#> Call:
#> lm(formula = Magical_Score ~ Nature_Score, data = u3)
#> 
#> Coefficients:
#>  (Intercept)  Nature_Score  
#>     3424.946         7.998

Collecting a new sample

Code 
u4 <- unicorns(500)
lm(Magical_Score ~ Nature_Score, u4)
#> 
#> Call:
#> lm(formula = Magical_Score ~ Nature_Score, data = u4)
#> 
#> Coefficients:
#>  (Intercept)  Nature_Score  
#>     3414.909         8.009

Replicating Processes

Code 
replicate(N, CODE)
  • N: number of times to repeat a process
  • CODE: what is to repeated

Extracting \(\hat \beta\) Coefficeints

Code 
b(MODEL, INDEX)
  • MODEL: a model that can be used to extract components
  • INDEX: which component do you want to use
    • 0: Intercept
    • 1: first slope
    • 2: second slope
    • ...

Collecting 1000 Samples

Code 
betas <- replicate(1000,
                   b(lm(Magical_Score ~ Nature_Score, unicorns(500)), 1))

betas
#>    [1] 7.999619 8.000680 7.999984 8.000473 7.996822 7.999667 7.998476 7.994427
#>    [9] 8.000400 8.000180 7.991096 8.004663 8.001771 7.998010 8.007847 8.002143
#>   [17] 7.997576 7.994148 8.000453 8.004216 8.003382 7.994335 8.000053 8.001225
#>   [25] 8.001973 8.000425 8.002658 7.998898 7.993388 7.997078 8.003194 7.996693
#>   [33] 8.001047 8.000292 8.000701 8.000692 8.001471 8.007882 7.999853 8.007126
#>   [41] 7.998198 7.998157 7.999286 8.001666 7.991880 8.008768 8.003644 7.996041
#>   [49] 8.003819 8.000639 8.010199 7.997813 7.995902 8.001633 7.995954 8.011122
#>   [57] 8.004849 7.998737 8.000236 7.998949 8.003761 8.000641 7.995459 7.997921
#>   [65] 8.006852 8.004086 7.999889 7.994307 7.996645 8.000272 8.004563 8.000832
#>   [73] 8.000942 8.003790 7.997582 7.995920 8.002142 8.009524 8.001072 8.006828
#>   [81] 8.000754 8.003015 8.005692 8.002430 7.996678 8.001948 7.995377 7.998517
#>   [89] 8.001960 7.994606 7.997573 7.999630 7.994502 8.004347 8.000093 8.000902
#>   [97] 8.001473 8.004295 7.995805 7.996390 8.003355 8.006944 8.005782 7.996836
#>  [105] 7.996817 8.004010 8.000917 8.002014 7.995494 7.998875 7.999354 8.002084
#>  [113] 7.998059 7.997758 8.002323 7.994843 8.000777 8.000376 8.000333 8.002607
#>  [121] 7.992622 7.995307 7.998806 8.004113 8.003079 8.005933 7.994439 8.006453
#>  [129] 7.997890 7.998079 8.000368 7.999780 7.998467 7.995373 8.004179 8.000057
#>  [137] 7.996682 8.004784 8.007202 7.999830 7.991969 8.005706 7.994626 8.003470
#>  [145] 7.998690 8.001567 7.998459 7.992117 7.995324 8.003352 7.997655 7.995583
#>  [153] 8.000042 8.005602 7.998236 7.999429 8.001406 7.995328 7.998828 7.996300
#>  [161] 7.996454 8.000910 7.998855 8.004106 7.993631 7.999822 7.996839 7.997085
#>  [169] 7.998157 7.999299 8.002709 8.009256 7.998106 7.999926 8.003312 7.993677
#>  [177] 8.007756 8.000571 7.991552 7.999053 8.011111 7.998970 7.998295 8.005105
#>  [185] 8.003479 7.987926 7.997472 8.003786 8.006721 7.997218 7.999919 7.998764
#>  [193] 8.002586 7.997666 7.997549 7.991979 8.001828 7.999028 8.003489 8.002961
#>  [201] 8.003455 7.999974 8.000590 7.999991 8.002332 7.999253 8.005414 7.999262
#>  [209] 7.999060 7.998186 8.002973 7.998032 8.002347 7.998331 8.003746 8.002150
#>  [217] 7.997281 8.003095 8.006593 7.996821 8.004268 7.998569 8.001343 8.007627
#>  [225] 7.999059 8.002810 8.002830 8.002333 8.001407 8.001689 8.001929 8.002401
#>  [233] 7.997709 8.002335 7.998244 7.996477 8.002823 8.007264 8.000086 8.002528
#>  [241] 8.002190 7.998752 8.000416 8.002722 8.000137 8.003034 8.000265 7.993565
#>  [249] 7.993509 7.998744 8.003030 8.004175 8.003938 7.995707 7.996536 8.008121
#>  [257] 8.002117 7.998014 8.000087 7.998504 8.003664 8.007215 8.001811 7.999076
#>  [265] 7.997219 8.008335 8.005202 8.006071 8.007045 7.996539 7.999589 8.005860
#>  [273] 8.004520 8.002544 8.005402 8.002325 7.995447 7.995449 8.007764 8.002900
#>  [281] 7.998703 8.001631 8.001210 7.998960 8.002063 7.994816 8.005033 8.002504
#>  [289] 8.005941 7.997182 7.997032 7.996257 8.005914 8.006604 7.995844 7.998264
#>  [297] 7.997588 7.996562 8.000694 7.992607 7.996916 7.999821 7.999886 8.004195
#>  [305] 7.995693 7.998228 8.005293 8.001849 8.005256 7.993044 7.996469 7.997849
#>  [313] 8.003826 7.999781 7.997511 7.988201 7.998125 7.995286 7.993599 7.994483
#>  [321] 7.999938 7.992511 8.001424 7.993820 7.996861 7.999384 7.996897 8.000544
#>  [329] 8.004206 8.002703 7.997575 7.998379 8.005910 8.003614 7.990586 8.006251
#>  [337] 7.998510 7.998536 7.995361 8.002728 7.993481 7.993334 8.000619 7.998357
#>  [345] 8.001394 7.993716 7.993536 8.003578 8.005082 8.005295 7.996715 8.002463
#>  [353] 7.998357 8.001986 7.992651 7.999159 8.007906 7.996685 7.998788 7.993418
#>  [361] 7.996608 7.997227 8.001205 8.001192 8.004436 8.000132 7.997705 8.000425
#>  [369] 8.001609 8.003462 7.999391 8.004268 7.997222 7.995462 7.991051 7.999655
#>  [377] 7.998679 7.994854 7.998218 8.001213 8.001355 8.002226 7.999865 8.000776
#>  [385] 7.999012 7.998432 8.005857 8.003251 7.999263 8.001103 7.995261 8.003481
#>  [393] 8.005188 8.001533 7.998749 8.002101 7.995054 8.003136 8.002512 7.994560
#>  [401] 7.995807 7.995372 7.997513 7.998702 8.002982 7.995366 8.003508 7.999357
#>  [409] 7.998794 7.998377 7.996880 8.005995 7.997436 8.001780 8.003903 8.002840
#>  [417] 8.002888 7.997339 8.001697 7.988533 7.997126 7.995107 7.996504 7.992989
#>  [425] 7.999529 7.994747 7.991229 7.999840 8.000415 8.007028 7.998598 8.001718
#>  [433] 8.004791 8.007827 8.001316 8.000870 8.008688 8.003047 8.000773 7.996666
#>  [441] 8.000331 7.995302 7.999705 8.002584 8.001179 7.994076 7.995395 7.998311
#>  [449] 7.993033 8.002681 8.005350 7.995099 7.997315 8.003288 7.997032 7.992718
#>  [457] 7.993538 8.002497 7.998935 7.999642 7.997054 7.997187 8.003429 7.999305
#>  [465] 7.998541 8.003920 8.001085 7.997146 8.002651 7.994471 7.996551 8.001507
#>  [473] 7.995907 8.005582 7.992678 8.001360 7.999244 7.998279 8.003482 7.997921
#>  [481] 7.994571 7.998326 7.996747 7.994873 8.011120 8.004748 8.000802 7.996510
#>  [489] 8.004941 7.998094 8.000777 8.005853 7.996064 7.989891 7.997768 8.000112
#>  [497] 8.002993 8.008579 7.999657 8.007115 8.006369 8.000290 7.996869 8.004906
#>  [505] 7.998172 8.010007 8.007165 7.989357 8.006293 8.003274 7.990845 7.996498
#>  [513] 8.004620 8.002109 8.002416 7.998333 7.998507 8.001153 8.006682 7.998084
#>  [521] 8.002828 7.997635 7.997115 8.000568 8.005599 8.000698 8.006763 7.999522
#>  [529] 8.001499 7.993632 8.004131 7.996480 8.007491 8.001195 8.000447 7.997227
#>  [537] 8.000987 7.996412 7.999687 7.993989 8.000841 8.007626 7.997970 7.998870
#>  [545] 8.002310 7.996737 7.994059 8.001197 8.002299 8.002330 8.007204 8.002636
#>  [553] 7.994555 7.996805 7.999139 8.003317 8.002507 7.995336 8.000961 8.001937
#>  [561] 7.995271 7.998278 7.996624 7.996960 8.000106 7.998788 8.003911 7.998335
#>  [569] 8.006035 8.000879 8.002948 8.000677 7.990234 8.006766 8.010774 8.005090
#>  [577] 7.999652 7.994030 7.999410 8.006888 8.000949 8.000035 7.995982 8.000322
#>  [585] 7.999938 8.002528 7.995494 8.005331 8.002157 8.004272 8.003083 8.008840
#>  [593] 7.998923 8.003014 8.000706 7.999009 7.997200 7.997876 7.997485 8.004241
#>  [601] 7.996730 8.005209 8.000935 8.004874 8.002648 8.002130 8.002340 7.994044
#>  [609] 8.002009 7.995816 7.998318 7.998445 8.001880 7.999366 8.002854 8.003744
#>  [617] 8.000313 8.003092 8.001229 7.992958 8.003976 7.995767 7.999384 8.000837
#>  [625] 8.000174 8.003985 8.000622 8.000634 7.994642 7.996744 7.995073 7.995932
#>  [633] 7.993150 7.999636 8.000047 8.009067 8.005276 8.000911 7.992700 7.997768
#>  [641] 7.998856 7.999329 8.008431 7.997752 7.999970 8.005375 8.003669 7.998744
#>  [649] 8.004052 7.996874 7.998751 8.005357 7.990729 7.996819 8.000867 8.005014
#>  [657] 7.997295 8.002054 7.997995 7.995154 7.998040 8.002961 8.008791 7.996920
#>  [665] 8.005368 8.002936 7.997955 7.996127 8.003900 8.004406 7.998640 8.001400
#>  [673] 7.997279 8.001245 7.999572 7.993229 7.997782 7.998208 7.992855 7.997820
#>  [681] 8.001538 8.003991 7.996852 8.004998 8.005100 7.999108 8.010044 8.005944
#>  [689] 7.999496 7.995893 7.997900 8.004777 8.004954 8.002988 8.006535 7.994029
#>  [697] 7.995976 7.999339 7.998131 8.001967 7.999537 8.009499 8.000084 7.997669
#>  [705] 7.999170 8.000081 8.002934 8.008022 8.002419 7.995815 7.996280 8.001102
#>  [713] 7.999217 8.012241 8.005100 8.008839 8.005161 8.001493 8.004494 7.999804
#>  [721] 8.005644 8.003844 8.008275 7.995872 7.997012 7.997363 7.996687 8.002608
#>  [729] 7.995762 7.998837 8.000661 8.000231 7.994237 7.998686 8.002868 7.995026
#>  [737] 7.998934 7.997725 8.002517 7.993810 8.001332 7.999005 8.008677 7.993150
#>  [745] 8.002854 7.995836 7.995853 7.996398 8.002133 8.000090 7.997974 7.999936
#>  [753] 8.000668 8.001790 8.005438 7.999452 8.001599 7.992016 8.006527 7.993558
#>  [761] 8.003888 8.003225 8.001702 7.999744 7.998187 8.004378 7.995874 8.001205
#>  [769] 7.994486 7.999730 7.998112 8.002247 7.994625 8.004080 7.997587 7.996924
#>  [777] 8.000029 7.999239 7.998319 7.999893 8.000885 7.999762 8.002675 7.998691
#>  [785] 7.999513 7.995506 7.996115 8.001306 8.004876 8.000892 8.001169 8.002285
#>  [793] 7.997692 7.992656 8.002263 7.992757 7.994324 8.003326 8.002751 7.995222
#>  [801] 8.004239 7.999157 8.004147 7.999743 7.997908 7.995517 7.999018 7.999859
#>  [809] 7.996671 7.998522 7.995266 8.000645 7.994868 8.003511 8.000823 7.999301
#>  [817] 7.996736 8.001545 7.996168 8.002118 7.995557 8.003081 8.003502 8.002224
#>  [825] 7.998246 7.998000 8.005204 7.997737 8.001626 8.000807 8.000998 7.994046
#>  [833] 8.001461 8.002668 7.998048 7.997664 7.997957 8.002652 7.999508 7.995026
#>  [841] 8.015261 8.002627 7.999462 7.997329 8.002419 8.001232 8.004855 7.993272
#>  [849] 7.994316 8.001439 7.994818 8.003476 7.998386 8.001803 7.997693 7.996715
#>  [857] 7.999228 8.000750 7.999004 7.991408 8.002875 8.004673 8.006064 8.005518
#>  [865] 7.997876 8.005514 7.993783 7.992365 8.000083 7.996425 8.003457 8.000626
#>  [873] 7.993767 8.002650 8.002397 8.000181 8.009504 7.997393 8.008419 7.999326
#>  [881] 7.997805 7.998424 7.997352 8.000634 8.005948 8.001557 8.002428 7.997441
#>  [889] 8.001458 7.993835 8.003225 8.002995 7.993931 8.003769 7.995695 8.006247
#>  [897] 7.993302 8.004054 8.005476 8.000710 8.005938 8.002549 7.994670 7.998287
#>  [905] 7.999881 7.999920 7.992778 7.997061 8.005836 7.999015 7.992395 8.004838
#>  [913] 7.997372 7.999597 7.998328 7.996903 8.001375 8.000688 7.997355 7.995171
#>  [921] 8.007068 8.002335 7.997872 7.998228 7.996271 8.003083 7.999884 7.994865
#>  [929] 7.991122 7.994631 8.003398 7.995791 7.998277 7.996653 7.993088 8.003222
#>  [937] 7.997416 7.997366 7.995508 8.002158 7.998012 7.995967 7.998326 7.998788
#>  [945] 8.000020 7.995044 7.993879 7.999909 7.996644 7.999959 7.989896 8.010432
#>  [953] 8.006583 7.997936 7.999628 7.997380 8.004261 8.003658 8.003810 7.995193
#>  [961] 8.005967 8.000446 8.005681 8.003800 7.998314 8.001728 8.002072 7.991659
#>  [969] 7.994770 7.999368 7.998948 8.001004 7.997555 7.997768 7.996578 7.996375
#>  [977] 8.000826 8.000687 7.998411 7.995293 7.993430 7.994025 8.004009 8.001455
#>  [985] 8.003077 7.996453 7.995144 8.006561 7.996461 7.998491 8.005694 7.998466
#>  [993] 7.996759 8.000251 7.997337 8.006188 8.001995 7.999805 7.992371 8.008856

Distributions of \(\hat \beta_1\)

Code 
ggplot(data.frame(x = betas), aes(x = x)) +
  geom_density()

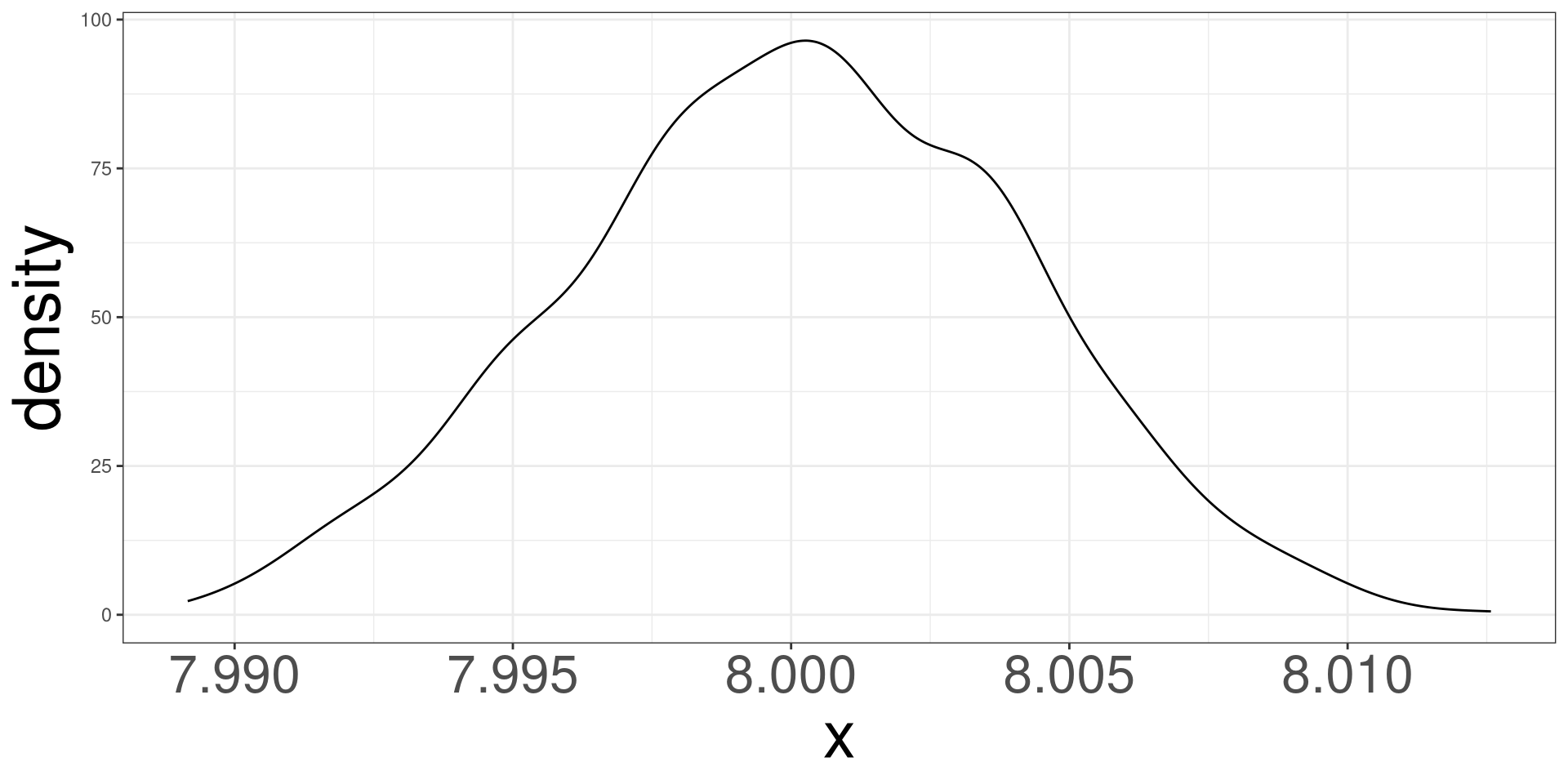
Central Limit Theorem

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Central Limit Theorem

The Central Limit Theorem (CLT) is a fundamental concept in probability and statistics. It states that the distribution of the sum (or average) of a large number of independent, identically distributed (i.i.d.) random variables will be approximately normal, regardless of the underlying distribution of those individual variables.

Formal Statement of the CLT

  • Let \(X_1\), \(X_2\), …, \(X_n\) be a sequence of i.i.d. random variables with mean \(\mu\) and standard deviation \(\sigma\).
  • Let \(\bar X\) be the sample mean of these variables.
  • As n (the sample size) approaches infinity, the distribution of \(\bar X\) approaches a normal distribution with:
    • Mean: \(\mu\)
    • Standard Deviation: \(\sigma/\sqrt{n}\)

CLT Example

  • Imagine: You’re flipping a fair coin many times.
    • Each flip is an independent event (heads or tails).
    • The probability of heads/tails is the same for each flip.
  • Now: Calculate the average number of heads after each set of 10 flips, then each set of 100 flips, and so on.
  • Observation: As the number of flips in each set increases, the distribution of these averages will start to resemble a bell-shaped curve (normal distribution), even though the individual coin flips are not normally distributed.

CLT Implications

  • Approximation: Even if the underlying data is not normally distributed, the distribution of the sample means will be approximately normal for large enough sample sizes.
  • Practical Rule: A common rule of thumb is that the sample size (n) should be at least 30 for the CLT to provide a good approximation. However, this is a guideline, and the actual required sample size can vary depending on the shape of the original distribution.

Normal Example \(n = 10\)

Simulating 500 samples of size 10 from a normal distribution with mean 5 and standard deviation of 2.

Code 
#rnorm(10, 5, 2)
sims <- replicate(500, rnorm(10, 5, 2))
sims_mean <- colMeans(sims)
ggplot(data.frame(x = sims_mean), aes(x)) +
  geom_density() +
  stat_function(fun = dnorm, 
                args = list(mean = 5, sd = 2 / sqrt(10)),
                col = "red")

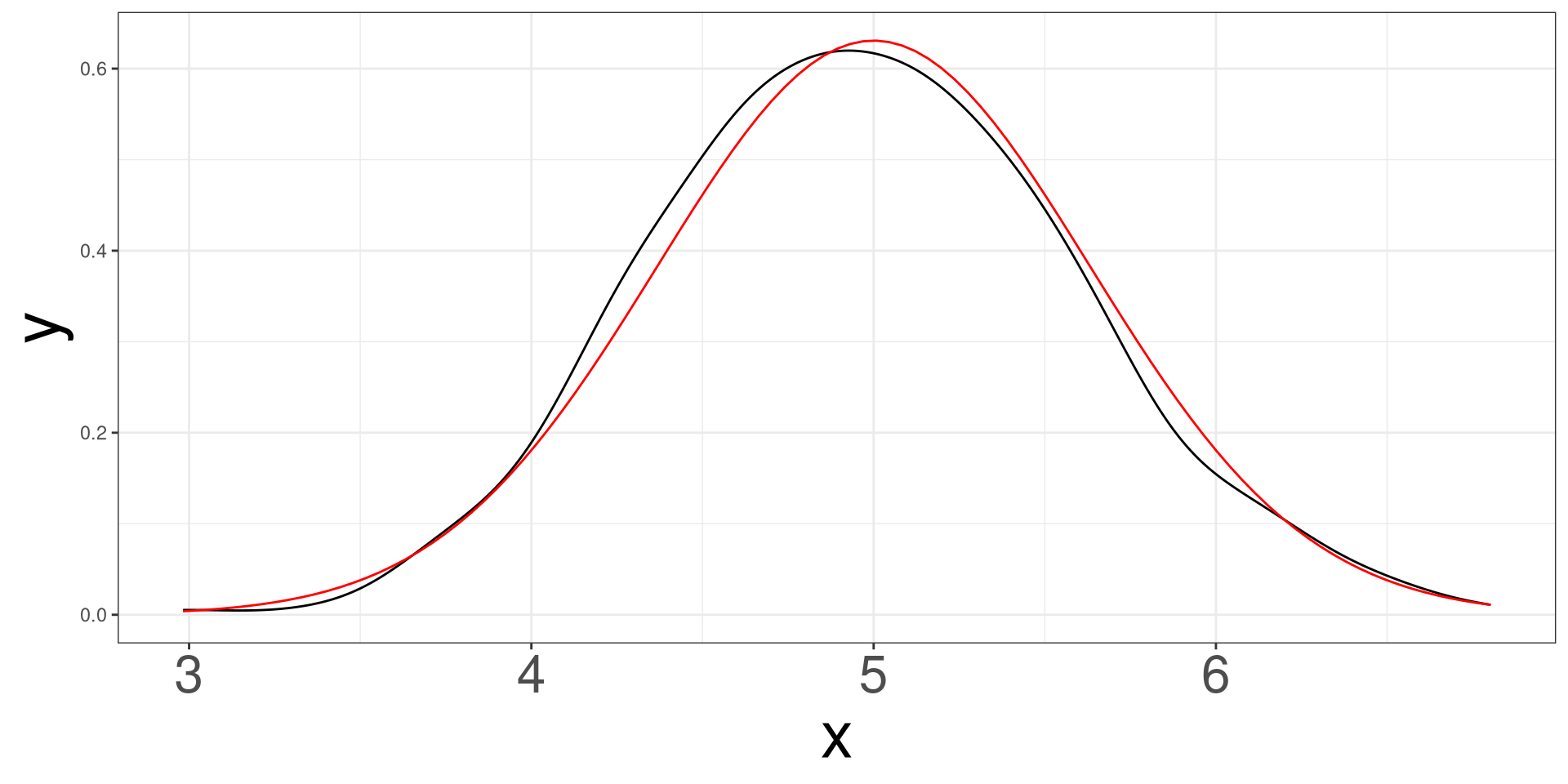
Normal Example \(n = 30\)

Simulating 500 samples of size 30 from a normal distribution with mean 5 and standard deviation of 2.

Code 
# rnorm(30, 5, 2)
sims <- replicate(500, rnorm(30, 5, 2))
sims_mean <- colMeans(sims)
ggplot(data.frame(x = sims_mean), aes(x)) +
  geom_density() +
  stat_function(fun = dnorm, 
                args = list(mean = 5, sd = 2 / sqrt(30)),
                col = "red")

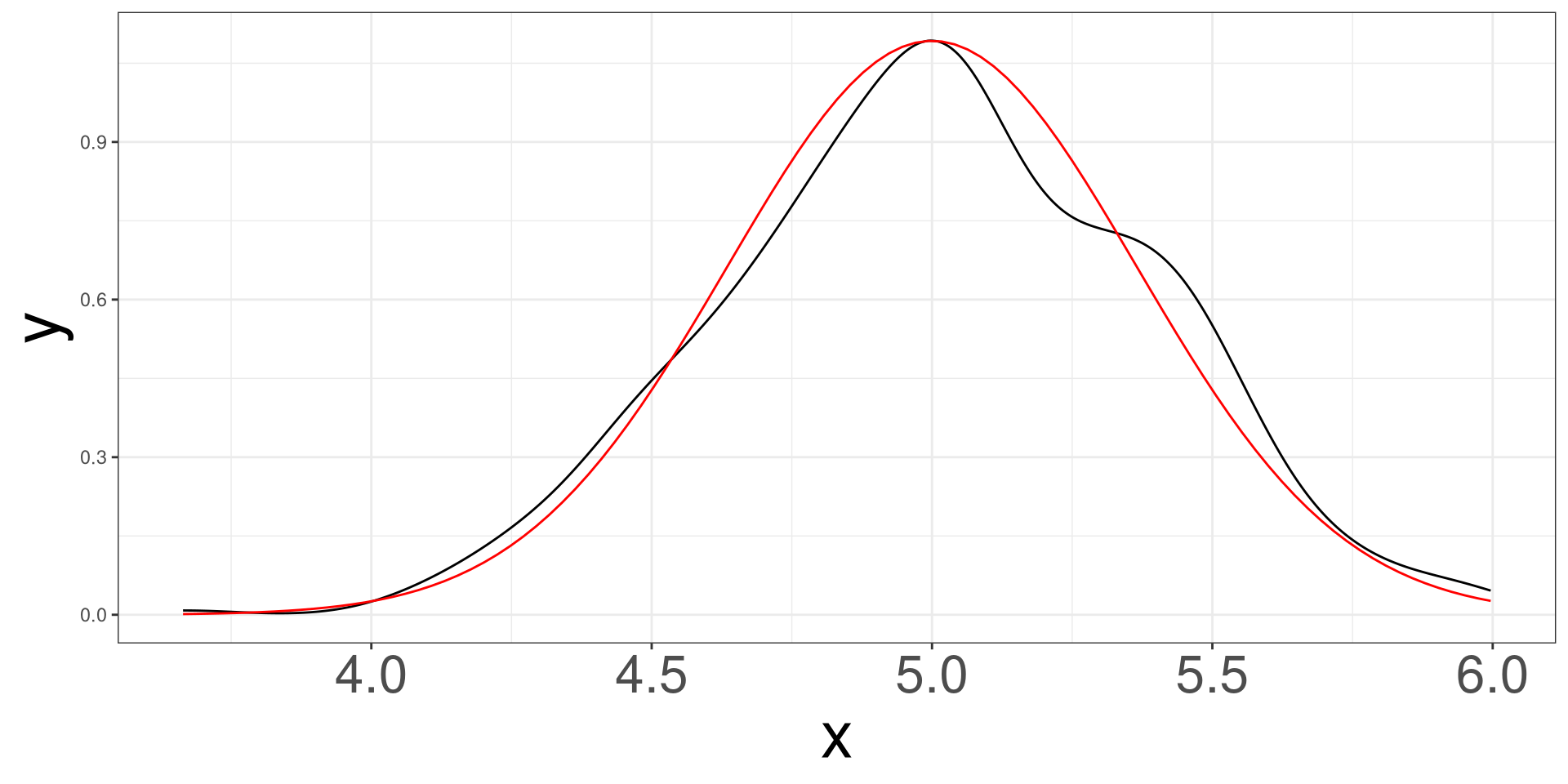
Normal Example \(n = 50\)

Simulating 500 samples of size 50 from a normal distribution with mean 5 and standard deviation of 2.

Code 
# rnorm(50, 5, 2)
sims <- replicate(500, rnorm(50, 5, 2))
sims_mean <- colMeans(sims)
ggplot(data.frame(x = sims_mean), aes(x)) +
  geom_density() +
  stat_function(fun = dnorm, 
                args = list(mean = 5, sd = 2 / sqrt(50)),
                col = "red")

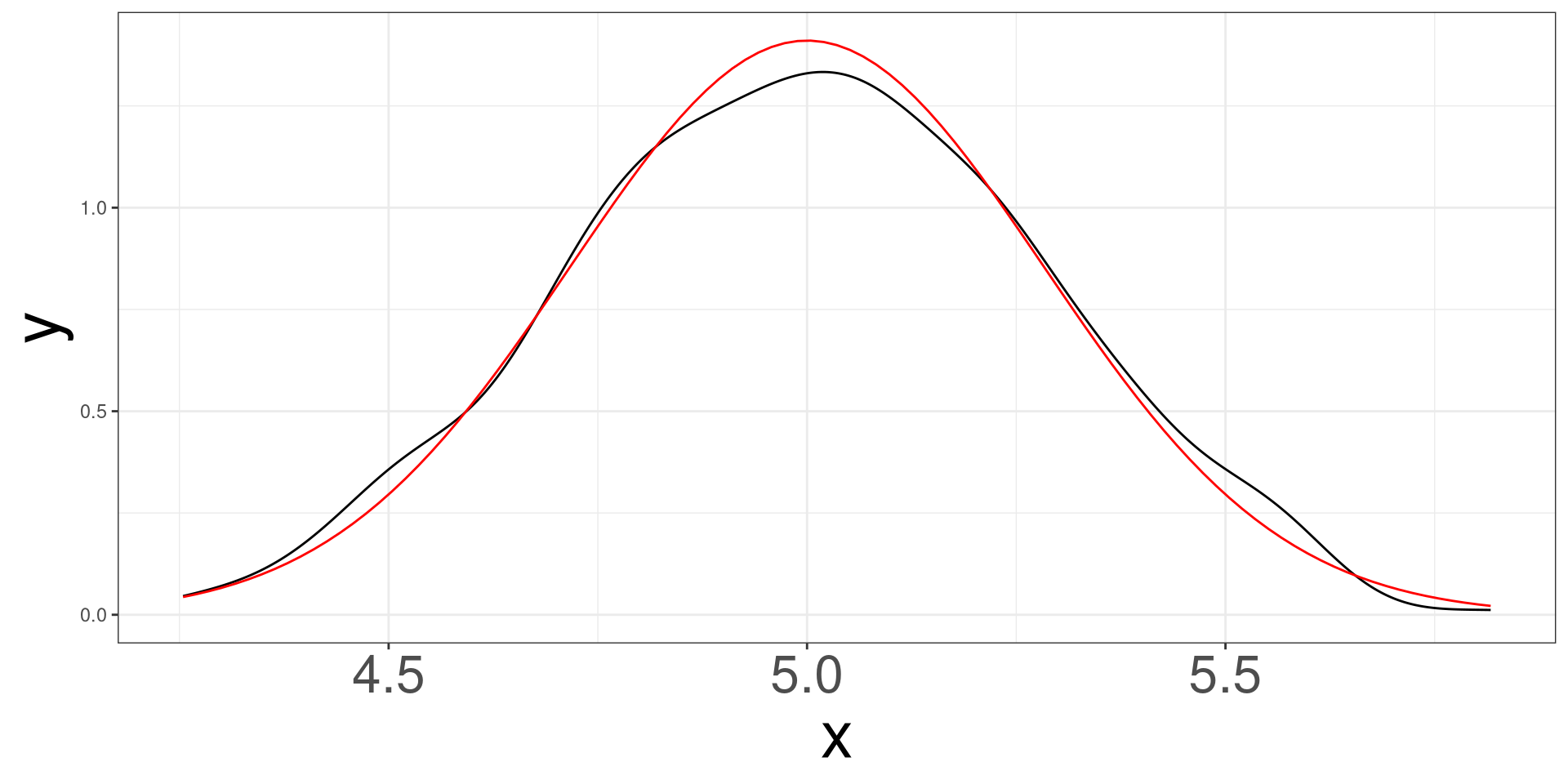
Normal Example \(n = 100\)

Simulating 500 samples of size 100 from a normal distribution with mean 5 and standard deviation of 2.

Code 
# rnorm(100, 5, 2)
sims <- replicate(500, rnorm(100, 5, 2))
sims_mean <- colMeans(sims)
ggplot(data.frame(x = sims_mean), aes(x)) +
  geom_density() +
  stat_function(fun = dnorm, 
                args = list(mean = 5, sd = 2 / sqrt(100)),
                col = "red")

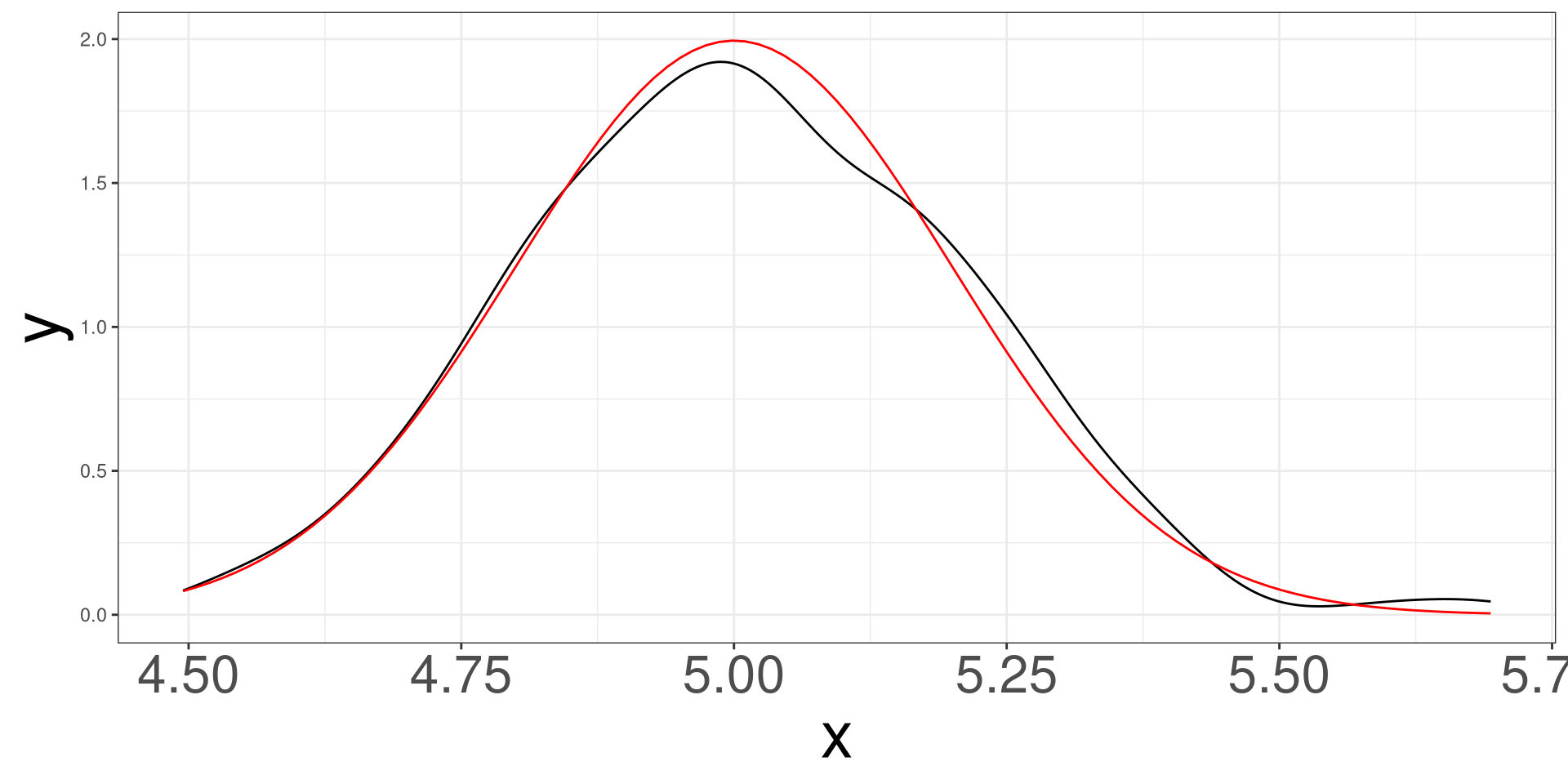
Common Sampling Distributions

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Normal DGP

When the data is said to have a normal distribution (DGP), there are special properties with both the mean and standard deviation, regardless of sample size.

Statistics

Mean \[ \bar X = \sum ^n_{i=1} X_i \]

Standard Deviation \[ s^2 = \frac{1}{n}\sum ^n_{i=1} (X_i - \bar X)^2 \]

When the true \(\mu\) and \(\sigma\) are known

A data sample of size \(n\) is generated from: \[ X_i \sim N(\mu, \sigma) \]

Distribution of \(\bar X\)

\[ \bar X \sim N(\mu, \sigma/\sqrt{n}) \]

Distribution of Z

\[ Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \sim N(0,1) \]

When the true \(\mu\) and \(\sigma\) are unknown

A data sample of size \(n\) is generated from: \[ X_i \sim N(\mu, \sigma) \]

Distribution of \(s^2\) (unknown \(\mu\))

\[ (n-1)s^2/\sigma^2 \sim \chi^2(n-1) \]

Distribution of Z (unknown \(\sigma\))

\[ Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \rightarrow \frac{\bar X - \mu}{s/\sqrt{n}} \sim t(n-1) \]

Sampling Distributions for Regression Models

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Regression Coefficients

The estimates of regression coefficients (slopes) have a distribution!

Based on our outcome, we will have 2 different distributions to work with: Normal or t.

Linear Regression

\[ \frac{\hat\beta_j-\beta_j}{\mathrm{se}(\hat\beta_j)} \sim t_{n-p^\prime} \]

\(\beta_j = 0\)

\[ \frac{\hat\beta_j}{\mathrm{se}(\hat\beta_j)} \sim t_{n-p^\prime} \]

Logistic Regression

\[ \frac{\hat\beta_j - \beta_j}{\mathrm{se}(\hat\beta_j)} \sim N(0,1) \]

\(\beta_j = 0\)

\[ \frac{\hat\beta_j}{\mathrm{se}(\hat\beta_j)} \sim N(0,1) \]

Scientific Notation

  • Sampling Distribution

  • Simulating Unicorns

  • Central Limit Theorem

  • Common Sampling Distributions

  • Sampling Distributions for Regression Models

  • Scientific Notation

Scientific Notation

We often work with very large or very small numbers.

  • Earth → Sun distance: 150,000,000 km
  • Diameter of a hydrogen atom: 0.0000000001 m

Problems with standard form:

  • Hard to read
  • Easy to copy wrong
  • Difficult to compare

Scientific notation makes numbers compact and standardized.

The Scientific Notation Form

A number is in scientific notation if:

\[ a \times 10^n \]

where:

  • \(a\) is at least 1 and less than 10
  • \(n\) is an integer (positive, negative, or zero)
  • \(10^n\) is a power of ten

Example: Large Number

Write 45,000 in scientific notation.

Move decimal:

\[ 45000 \rightarrow 4.5 \]

Moved 4 places left:

\[ 4.5 \times 10^4 \]

Example: Small Number

Write 0.00072 in scientific notation.

Move decimal:

\[ 0.00072 \rightarrow 7.2 \]

Moved 4 places right:

\[ 7.2 \times 10^{-4} \]

Understanding Positive Exponent

Positive exponents → big numbers

  • \(10^3 = 1{,}000\)
  • \(10^6 = 1{,}000{,}000\)

Example:

\[ 2.1 \times 10^6 = 2{,}100{,}000 \]

Understanding Negative Exponent

Negative exponents → small numbers

  • \(10^{-2} = 0.01\)
  • \(10^{-5} = 0.00001\)

Example:

\[ 4.3 \times 10^{-3} = 0.0043 \]

Converting Back to Standard Form

Rule:

  • \(10^{+n}\): move decimal right \(n\) places
  • \(10^{-n}\): move decimal left \(n\) places

Convert Example (Positive Exponent)

\[ 6.2 \times 10^5 \]

Move decimal 5 places right:

\[ 620{,}000 \]

Convert Example (Negative Exponent)

\[ 9.1 \times 10^{-4} \]

Move decimal 4 places left:

\[ 0.00091 \]

Comparing Numbers in Scientific Notation

Step 1: Compare exponents

  • Bigger exponent → bigger number

Step 2: If exponents match, compare coefficients \(a\)

Example:

  • \(3.2 \times 10^5\)
  • \(7.1 \times 10^4\)

Since \(10^5 > 10^4\), the first number is larger.

Scientific Notation in R

R often displays very large/small numbers using e notation.

\[ a \times 10^n \quad \text{is shown as} \quad a\text{e}n \]

Examples:

  • 3e+06 means \(3 \times 10^6\)
  • 4.5e-04 means \(4.5 \times 10^{-4}\)